题目内容
2.一个篮球运动员投篮一次得3分的概率为a,得2分的概率为b,不得分的概率为c(a,b,c∈(0,1)),已知他投篮一次得分的数学期望为2,则$\frac{2}{a}+\frac{1}{3b}$的最小值为( )| A. | $\frac{32}{3}$ | B. | $\frac{28}{3}$ | C. | $\frac{16}{3}$ | D. | 4 |
分析 由题意可得:3a+2b+0•c=2,即3a+2b=2.a,b,c∈(0,1)),再利用“乘1法”与基本不等式的性质即可得出.
解答 解:由题意可得:3a+2b+0•c=2,即3a+2b=2.a,b,c∈(0,1)),
∴$\frac{2}{a}+\frac{1}{3b}$=$\frac{1}{2}(3a+2b)$$(\frac{2}{a}+\frac{1}{3b})$=$\frac{1}{2}(\frac{20}{3}+\frac{4b}{a}+\frac{a}{b})$$≥\frac{1}{2}$$(\frac{20}{3}+2\sqrt{\frac{4b}{a}•\frac{a}{b}})$=$\frac{16}{3}$,当且仅当a=2b=$\frac{1}{2}$时取等号.
故选:C.
点评 本题考查了数学期望计算公式、“乘1法”与基本不等式的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
13.已知数列{an}是等差数列,其前n项和为Sn,若a2a3a4=21,且$\frac{15}{{{S_3}{S_5}}}+\frac{35}{{{S_5}{S_7}}}+\frac{21}{{{S_7}{S_3}}}=\frac{3}{7}$.则a3等于( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | 2 | D. | 3 |
10.将函数$y=2sin(2x+\frac{π}{6})$的图象向左平移$\frac{1}{4}$个周期后,所得图象对应的函数为( )
| A. | $y=2sin(2x+\frac{2π}{3})$ | B. | $y=2sin(2x+\frac{5π}{12})$ | C. | $y=2sin(2x-\frac{π}{3})$ | D. | $y=2sin(2x-\frac{π}{12})$ |
17.复数z=$\frac{2{i}^{2}+4}{i+1}$的虚部为( )
| A. | -3 | B. | -1 | C. | 1 | D. | 2 |
14.按照图中的程序框图执行,若M处条件是k>16,则输出结果为( )
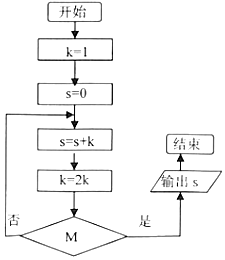

| A. | 15 | B. | 16 | C. | 31 | D. | 32 |
11.函数y=$\frac{1}{x}$+$\frac{1}{3-x}$(0<x<3)的最小值为( )
| A. | 1 | B. | $\frac{4}{3}$ | C. | $\frac{5}{3}$ | D. | 2 |
12.已知抛物线C:y2=4x的焦点为F,准线为l,过点F的直线交抛物线于A,B两点(A在第一象限),过点A作准线l的垂线,垂足为E,若∠AFE=60°,则△AFE的面积为( )
| A. | $4\sqrt{3}$ | B. | $2\sqrt{3}$ | C. | $\frac{{4\sqrt{3}}}{3}$ | D. | $\frac{{2\sqrt{3}}}{3}$ |