题目内容
已知函数f(x)=x2-2ax-2alnx(a∈R,a≠0),则下列说法错误的是( )
| A、若a<0,则f(x)有零点 | ||
B、若f(x)有零点,则a≤
| ||
| C、?a>0使得f(x)有唯一零点 | ||
D、若f(x)有唯一零点,则a≤
|
考点:命题的真假判断与应用,函数的零点
专题:阅读型,函数的性质及应用
分析:先将方程f(x)=0进行参变量分离,得到2a=
,令g(x)=
,转化成y=2a与y=g(x)的图象的交点个数,利用导数得到函数的单调性,结合函数的图象可得A,C,D都正确,B错误.
| x2 |
| x+lnx |
| x2 |
| x+lnx |
解答:
解:令f(x)=x2-2ax-2alnx=0,则2a(x+lnx)=x2,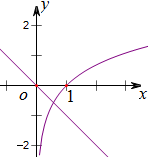
∴2a=
,令g(x)=
,
则g′(x)=
=
令h(x)=x+lnx,通过作出两个函数y=lnx及y=-x的图象(如右图)
发现h(x)有唯一零点在(0,1)上,
设这个零点为x0,当x∈(0,x0)时,g′(x)<0,g(x)在(0,x0)上单调递减,x=x0是渐近线,
当x∈(x0,1)时,g′(x)<0,则g(x)在(x0,1)上单调递减,
当x∈(1,+∞)时g′(x)>0,g(x)在(1,+∞)单调递增,
∴g(1)=1,可以作出g(x)=
的大致图象,
结合图象可知,当a<0时,y=2a与y=g(x)的图象只有一个交点,则函数y=f(x)只有一个零点,故选项A正确;
若函数y=f(x)有零点,则a<0或a≥
,故选项B不正确;
存在a=
>0,函数y=f(x)有唯一零点,故选项C正确;
若函数y=f(x)有唯一零点,则a=
或a<0,则a≤
且a≠0,故选项D正确.
故选:B.

∴2a=
| x2 |
| x+lnx |
| x2 |
| x+lnx |
则g′(x)=
2x(x+lnx)-x2(1+
| ||
| (x+lnx)2 |
| x(x-1+2lnx) |
| (x+lnx)2 |
令h(x)=x+lnx,通过作出两个函数y=lnx及y=-x的图象(如右图)
发现h(x)有唯一零点在(0,1)上,
设这个零点为x0,当x∈(0,x0)时,g′(x)<0,g(x)在(0,x0)上单调递减,x=x0是渐近线,
当x∈(x0,1)时,g′(x)<0,则g(x)在(x0,1)上单调递减,
当x∈(1,+∞)时g′(x)>0,g(x)在(1,+∞)单调递增,

∴g(1)=1,可以作出g(x)=
| x2 |
| x+lnx |
结合图象可知,当a<0时,y=2a与y=g(x)的图象只有一个交点,则函数y=f(x)只有一个零点,故选项A正确;
若函数y=f(x)有零点,则a<0或a≥
| 1 |
| 2 |
存在a=
| 1 |
| 2 |
若函数y=f(x)有唯一零点,则a=
| 1 |
| 2 |
| 1 |
| 2 |
故选:B.
点评:本题考查了函数的零点与方程根的关系.函数的零点等价于对应方程的根,等价于函数的图象与x轴交点的横坐标,解题时要注意根据题意合理的选择转化.常运用数形结合的数学思想方法.属于中档题.

练习册系列答案
相关题目
直线y=-
x-
和直线y=
x-
平行,则m的值为( )
| 1 |
| m |
| 6 |
| m |
| 2-m |
| 3 |
| 2m |
| 3 |
| A、-1或3 | B、-1 |
| C、-3 | D、1或-3 |
若定义在R上的偶函数f(x)满足“对任意x1,x2∈(-∞,0),当x1-x2<0时,都有f(x1)-f(x2)<0”,则a=f(-2)与b=f(3)的大小关系为( )
| A、a>b | B、a<b |
| C、a=b | D、不确定 |
把函数y=
cosx-sinx的图象向右平移a个单位,所得图象关于y轴对称,则a的最大负值是( )
| 3 |
A、-
| ||
B、-
| ||
C、-
| ||
D、-
|
已知等差数列{an}的前n项和为Sn,且满足S3≤6,S4≥8,S6≤20,当a4取得最大值时,数列{an}的公差为( )
| A、4 | ||
B、
| ||
C、
| ||
D、
|
下列各组函数表示同一个函数的是( )
A、y=x+1与y=
| |||||||
B、y=x与y=
| |||||||
C、y=
| |||||||
D、y=
|