题目内容
已知函数f(x)=
,则下列关于函数y=f[f(kx)+1]+1(k≠0)的零点个数的判断正确的是( )
|
| A、当k>0时,有3个零点;当k<0时,有4个零点 |
| B、当k>0时,有4个零点;当k<0时,有3个零点 |
| C、无论k为何值,均有3个零点 |
| D、无论k为何值,均有4个零点 |
考点:函数零点的判定定理
专题:计算题,函数的性质及应用
分析:函数y=f[f(kx)+1]+1(k≠0)的零点个数即方程f[f(kx)+1]+1=0的解的个数,从而解方程可得.
解答:
解:令f[f(kx)+1]+1=0得,
或
解得,f(kx)+1=0或f(kx)+1=
;
由f(kx)+1=0得,
或
;
即x=0或kx=e;
由f(kx)+1=
得,
或
;
即ekx=1+
,(无解)或kx=e
-1;
综上所述,x=0或kx=e或kx=e
-1;
故无论k为何值,均有3个解;
故选C.
|
|
解得,f(kx)+1=0或f(kx)+1=
| 1 |
| e |
由f(kx)+1=0得,
|
|
即x=0或kx=e;
由f(kx)+1=
| 1 |
| e |
|
|
即ekx=1+
| 1 |
| e |
| 1 |
| e |
综上所述,x=0或kx=e或kx=e
| 1 |
| e |
故无论k为何值,均有3个解;
故选C.
点评:本题考查了函数的零点与方程的根的关系应用,属于基础题.

练习册系列答案
相关题目
 棱长为2的正方体被一平面截得的几何体的三视图如图所示,那么被截去的几何体的体积是( )
棱长为2的正方体被一平面截得的几何体的三视图如图所示,那么被截去的几何体的体积是( )A、
| ||
B、
| ||
| C、4 | ||
| D、3 |
如图,网格纸上小正方形边长为1,粗线画出的是某几何体的三视图,则该几何体的体积为( )

| A、8 | B、12 | C、4 | D、6 |
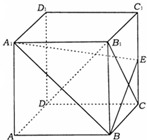 长方体ABCD-A1B1C1D1中,AA1=2,BC=
长方体ABCD-A1B1C1D1中,AA1=2,BC=