题目内容
过椭圆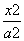 +
+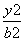 =1(a>b>0)的左顶点A作斜率为2的直线,与椭圆的另一个交点为B,与y轴的交点为C,已知
=1(a>b>0)的左顶点A作斜率为2的直线,与椭圆的另一个交点为B,与y轴的交点为C,已知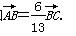
(1)求椭圆的离心率;
(2)设动直线y=kx+m与椭圆有且只有一个公共点P,且与直线x=4相交于点Q,若x轴上存在一定点M(1,0),使得PM⊥QM,求椭圆的方程.
解:(1)∵A(-a,0),设直线方程为y=2(x+a),B(x1,y1).
令x=0,则y=2a,∴C(0,2a),
 ∴x1+a=
∴x1+a= (-x1),y1=
(-x1),y1= (2a-y1),
(2a-y1),
整理,得x1=- a,y1=
a,y1= a.
a.
∵B点在椭圆上,
 ∴
∴ =
= ,
,
∴ =
= ,即1-e2=
,即1-e2= ,
,
∴e=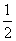 .
.
(2)∵ =
= ,可设b2=3t,a2=4t,
,可设b2=3t,a2=4t,
∴椭圆的方程为3x2+4y2-12t=0.
由 得
得
(3+4k2)x2+8kmx+4m2-12t=0.
∵动直线y=kx+m与椭圆有且只有一个公共点P,
∴Δ=0,即64k2m2-4(3+4k2)(4m2-12t)=0,整理得m2=3t+4k2t.
设P(x1,y1),
 又Q(4,4k+m),x轴上存在一定点M(1,0),使得PM⊥QM,
又Q(4,4k+m),x轴上存在一定点M(1,0),使得PM⊥QM,
∴ ·(-3,-(4k+m))=0恒成立.
·(-3,-(4k+m))=0恒成立.
整理,得3+4k2=m2,
∴3+4k2=3t+4k2t恒成立.
故t=1,所求椭圆方程为 +
+ =1.
=1.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,
, 。
。 的值为
的值为 

 B.
B. C.
C. D.
D. .
. 中,
中, ,则点
,则点 到平面
到平面 的距离为
的距离为 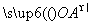 +
+ =0(O为坐标原点),
=0(O为坐标原点),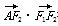 =0,若椭圆的离心率等于
=0,若椭圆的离心率等于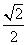 ,则直线AB的方程是( )
,则直线AB的方程是( )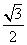 x D.y=
x D.y=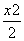 +y2=1的左焦点,点P为椭圆C上任意一点,点Q的坐标为(4,3),则|PQ|+|PF|取最大值时,点P的坐标为________.
+y2=1的左焦点,点P为椭圆C上任意一点,点Q的坐标为(4,3),则|PQ|+|PF|取最大值时,点P的坐标为________. B.
B.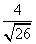
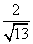 D.
D.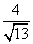
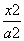 +
+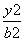 =1(a>b>0)上的任意一点,若∠PF1F2=α,∠PF2F1=β,且cos α=
=1(a>b>0)上的任意一点,若∠PF1F2=α,∠PF2F1=β,且cos α=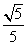 ,sin(α+β)=
,sin(α+β)=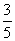 ,则此椭圆的离心率为________.
,则此椭圆的离心率为________. 的前
的前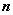 项和
项和 满足:
满足: ,等比数列
,等比数列 的前
的前 ,公
,公 ,且
,且 .
. 的前
的前 ,求证:
,求证: