题目内容
设数列 的前
的前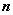 项和
项和 满足:
满足: ,等比数列
,等比数列 的前
的前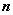 项和为
项和为 ,公
,公
比为 ,且
,且 .
.
(1)求数列 的通项公式; (2)设数列
的通项公式; (2)设数列 的前
的前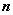 项和为
项和为 ,求证:
,求证:
解:(1)∵ ………①, ∴
………①, ∴ ………②
………②
②-①得, ,∴
,∴ ……………………3分
……………………3分
又∵等比数列 ,
, ,∴
,∴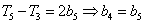 ,
, ,∴
,∴
∴数列 是1为首项,4为公差的等差数列,∴
是1为首项,4为公差的等差数列,∴ ……6分
……6分
(2)由(1)可得 ……………………8分
……………………8分
∴ ……………………10分
……………………10分

 在
在 时单调递增,∴
时单调递增,∴ ,即
,即 …………12分
…………12分

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
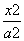 +
+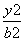 =1(a>b>0)的左顶点A作斜率为2的直线,与椭圆的另一个交点为B,与y轴的交点为C,已知
=1(a>b>0)的左顶点A作斜率为2的直线,与椭圆的另一个交点为B,与y轴的交点为C,已知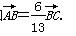
 ,
, ,若直线
,若直线 与
与 关于
关于 对称,则
对称,则 B.
B. C.
C. D.
D.
 (t为参数),C在点(1,1)处的切线为l,以坐标原点为极点,以x轴的正半轴为极轴建立极坐标系,则l的极坐标方程为
(t为参数),C在点(1,1)处的切线为l,以坐标原点为极点,以x轴的正半轴为极轴建立极坐标系,则l的极坐标方程为  的最小正周期是 ( )
的最小正周期是 ( ) B、
B、 C、
C、 D、
D、
 ( )
( ) B、
B、 C、
C、 D、
D、
 的实数解落在的区间是 ( )
的实数解落在的区间是 ( )



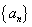 是等差数列,其前
是等差数列,其前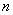 项和为
项和为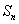 ,
,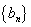 是等比数列,且
是等比数列,且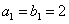 ,
,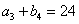 ,
,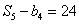 .
.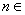 N
N ,是否存在正实数
,是否存在正实数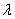 ,使不等式
,使不等式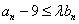 恒成立,若存在,求出
恒成立,若存在,求出