题目内容
已知两个实数a,b(a≠b),满足aea=beb.命题p:lna+a=lnb+b;命题q:(a+1)(b+1)>0,则下列命题正确的是( )
| A、p真q假 | B、p假q真 |
| C、p真q真 | D、p假q假 |
考点:复合命题的真假
专题:导数的综合应用,简易逻辑
分析:考察函数f(x)=xex,在x∈R上的单调性即可判断出p,q的真假.
解答:
解:考察函数f(x)=xex,x∈R,f′(x)=(x+1)ex,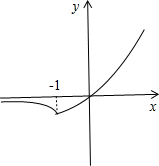
令f′(x)>0,解得x>-1,此时函数f(x)单调递增;令f′(x)<0,解得x<-1,此时函数f(x)单调递减.
∴当x=-1时,函数f(x)取得极小值即最小值,∴f(x)≥f(-1)=-
.
对于命题p:由于a<0,b<0,lna+a=lnb+b不可能成立,因此是假命题;
对于命题q:a<-1,0>b>-1,则(a+1)(b+1)<0,因此q也是假命题.
综上可得:p,q都是假命题.
故选:D.

令f′(x)>0,解得x>-1,此时函数f(x)单调递增;令f′(x)<0,解得x<-1,此时函数f(x)单调递减.
∴当x=-1时,函数f(x)取得极小值即最小值,∴f(x)≥f(-1)=-
| 1 |
| e |
对于命题p:由于a<0,b<0,lna+a=lnb+b不可能成立,因此是假命题;
对于命题q:a<-1,0>b>-1,则(a+1)(b+1)<0,因此q也是假命题.
综上可得:p,q都是假命题.
故选:D.
点评:本题考查了利用导数研究函数的单调性、简易逻辑的判定,考查了推理能力与计算能力,属于难题.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
已知实数x,y满足
,则z=-3x+2y的最大值为( )
|
| A、-4 | B、2 | C、4 | D、6 |
已知等比数列{an},则“a1<a2<a3”是“{an}为递增数列”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
若sin2α=
,则
cos(
+α)的值为( )
| 24 |
| 25 |
| 2 |
| π |
| 4 |
A、
| ||
B、
| ||
C、±
| ||
D、±
|