题目内容
曲线y=x3+11在点P（1，12）处的切线与y轴交点的纵坐标是 ．
考点：利用导数研究曲线上某点切线方程
专题：计算题,圆锥曲线的定义、性质与方程
分析：根据导数的几何意义求出函数f（x）在x=1处的导数，从而求出切线的斜率，再用点斜式写出切线方程，化成一般式，最后令x=0解得的y即为曲线y=x3+11在点P（1，12）处的切线与y轴交点的纵坐标．
解答：
解：∵y=x3+11，∴y′=3x2
则y′|x=1=3x2|x=1=3．
∴曲线y=x3+11在点P（1，12）处的切线方程为y-12=3（x-1），即3x-y+9=0．
令x=0，解得y=9．
∴曲线y=x3+11在点P（1，12）处的切线与y轴交点的纵坐标是9．
故答案为：9．
则y′|x=1=3x2|x=1=3．
∴曲线y=x3+11在点P（1，12）处的切线方程为y-12=3（x-1），即3x-y+9=0．
令x=0，解得y=9．
∴曲线y=x3+11在点P（1，12）处的切线与y轴交点的纵坐标是9．
故答案为：9．
点评：本题主要考查了利用导数研究曲线上某点切线方程，以及直线与坐标轴的交点坐标等有关问题，属于基础题．
练习册系列答案
相关题目
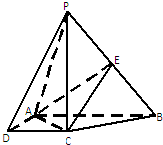如图，在四棱锥P-ABCD中，PC⊥底面ABCD，ABCD是直角梯形，AB⊥AD，AB∥CD，AB=2AD=2CD=2，E是PB的中点．（1）求证：EC∥平面PAD
（2）求证：平面EAC⊥平面PBC．