题目内容
已知sin2x+2sinxcosx-3cos2x=m-1，则实数m的取值范围为 ．
考点：两角和与差的正弦函数,二倍角的余弦
专题：三角函数的图像与性质
分析：先根据已知条件求得m的表达式，进而根据两角和公式和二倍角公式对其进行整理，最后利用三角函数的图象和性质求得其最大和最小值．
解答：
解：∵sin2x+2sinxcosx-3cos2x=m-1，
∴m=sin2x+2sinxcosx-3cos2x+1
=-cos2x+sin2x-cos2x
=sin2x-2cos2x，
=
sin（2x+φ），（其中tanφ=-2），
∴-
≤m≤
，
故答案为：[-
，
]．
∴m=sin2x+2sinxcosx-3cos2x+1
=-cos2x+sin2x-cos2x
=sin2x-2cos2x，
=
| 5 |
∴-
| 5 |
| 5 |
故答案为：[-
| 5 |
| 5 |
点评：本题主要考查了两角和公式的正弦函数，二倍角公式的应用．考查了学生对基础知识的综合运用．
练习册系列答案
星级口算天天练系列答案
芒果教辅达标测试卷系列答案
相关题目
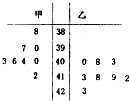为调查甲乙两人网站受欢迎的程度，随机选取了某个月1号至8号，统计这8天内每天同一时间段的点击量，得到如图所示的茎叶图．