题目内容
 如图,在四面体ABCD中,E、F分别是AB、AC的中点,过直线EF做平面α,分别交BD于M、交CD于N.求证:EF∥MN.
如图,在四面体ABCD中,E、F分别是AB、AC的中点,过直线EF做平面α,分别交BD于M、交CD于N.求证:EF∥MN.考点:空间中直线与直线之间的位置关系
专题:空间位置关系与距离
分析:利用线面平行的判定和性质定理解答.由EF∥BC可得,EF∥平面BCD,平面EFNM过EF,与平面BCD交于MN,得到EF∥MN.
解答:
证明:∵E、F分别是AB、AC的中点,
∴EF∥BC,
并且EF?平面BCD,BC?平面BCD,
∴EF∥平面BCD,
又EF?平面EFNM,平面EFNM∩平面BCD=MN,
∴EF∥MN.
∴EF∥BC,
并且EF?平面BCD,BC?平面BCD,
∴EF∥平面BCD,
又EF?平面EFNM,平面EFNM∩平面BCD=MN,
∴EF∥MN.
点评:本题考查了线面平行的判定定理和性质定理的运用,体现了转化的思想.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
已知抛物线y2=2px(p>0)上一点M(1,m)(m>0)到其焦点F的距离为5,该抛物线的顶点在直线MF上的射影为点P,则点P的坐标为( )
A、(
| ||||
B、(
| ||||
C、(
| ||||
D、(
|
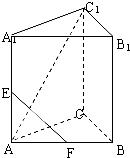 如图,在正三棱柱ABC-A1B1C1中,AC=2,AC1与底面成60°角,E、F分别为AA1、AB的中点.
如图,在正三棱柱ABC-A1B1C1中,AC=2,AC1与底面成60°角,E、F分别为AA1、AB的中点.