题目内容
17.某同学用“五点法”画函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)在某一周期内的图象时,列表并填入了部分数据,如表:| ωx+φ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| x | $\frac{π}{3}$ | $\frac{5π}{6}$ | |||
| Asin(ωx+φ) | 0 | $\sqrt{2}$ | -$\sqrt{2}$ | 0 |
(Ⅱ)求函数f(x)在区间[-$\frac{π}{2}$,0]上的最大值和最小值.
分析 (Ⅰ)利用五点法作图,将表格数据补充完整,并求得函数f(x)=Asin(ωx+φ)的解析式.
(Ⅱ)根据x的取值范围,求出2x-$\frac{π}{6}$的取值范围,计算sin(2x-$\frac{π}{6}$)的取值范围,即得f(x)的最大最小值.
解答 (本题满分为12分)
解 (Ⅰ)根据表中已知数据可得:A=$\sqrt{2}$,$\frac{π}{3}$ω+φ=$\frac{π}{2}$,$\frac{5π}{6}$ω+φ=$\frac{3π}{2}$,
解得ω=2,φ=-$\frac{π}{6}$.数据补全如下表:
| ωx+φ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| x | $\frac{π}{12}$ | $\frac{π}{3}$ | $\frac{7π}{12}$ | $\frac{5π}{6}$ | $\frac{13π}{12}$ |
| Asin(ωx+φ) | 0 | $\sqrt{2}$ | 0 | -$\sqrt{2}$ | 0 |
(Ⅱ)∵x∈[-$\frac{π}{2}$,0]时,
∴2x-$\frac{π}{6}$∈[-$\frac{7π}{6}$,-$\frac{π}{6}$],
当2x-$\frac{π}{6}$=-$\frac{π}{2}$,即x=-$\frac{π}{6}$时,sin(2x-$\frac{π}{6}$)=-1,
∴f(x)取得最小值-$\sqrt{2}$;
当2x-$\frac{π}{6}$=-$\frac{7π}{6}$,即x=-$\frac{π}{2}$时,sin(2x-$\frac{π}{6}$)=sin(-$\frac{7π}{6}$)=$\frac{1}{2}$,
∴f(x)取得最大值$\sqrt{2}$×$\frac{1}{2}$=$\frac{\sqrt{2}}{2}$;
∴函数f(x)在区间[-$\frac{π}{2}$,0]上的最大值是$\frac{\sqrt{2}}{2}$,最小值是-$\sqrt{2}$.
点评 本题主要考查了用五点法作函数f(x)=Asin(ωx+φ)在一个周期上的简图,由y=Asin(ωx+φ)的部分图象确定其解析式,正弦函数的最值,属于基础题.

练习册系列答案
相关题目
7.已知抛物线x2=2py(p>0)的准线经过点(0,-2),则抛物线的焦点坐标为( )
| A. | (0,1) | B. | (0,2) | C. | (1,0) | D. | (2,0) (第4题图) |
8.设函数$f(x)=ln(1+|x|)-\frac{1}{{1+{x^2}}}$则使f(2x)>f(x-1)成立的x范围为( )
| A. | $(-∞,-1)∪(\frac{1}{3},+∞)$ | B. | $(-1,\frac{1}{3})$ | C. | $(-∞,\frac{1}{3})∪(1,+∞)$ | D. | $(\frac{1}{3},1)$ |
5.设a=log${\;}_{\frac{1}{3}}$6,b=($\frac{1}{4}$)0.8,c=lnπ,下列结论正确的是( )
| A. | a<b<c | B. | a<c<b | C. | c<a<b | D. | b<a<c |
2.已知平面向量$\overrightarrow{a}$=(1,2),$\overrightarrow b$=(x,-2),若$\overrightarrow a$与$\overrightarrow b$共线,则x的值为( )
| A. | -4 | B. | 4 | C. | -1 | D. | 1 |
9.已知函数f(x)=x2-2x在区间[-1,t]上的最大值为3,则实数t的取值范围是( )
| A. | (1,3] | B. | [1,3] | C. | [-1,3] | D. | (-1,3] |
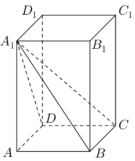 如图,长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=3;
如图,长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=3;