题目内容
6．
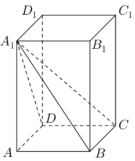如图，长方体ABCD-A1B1C1D1中，AB=BC=2，AA1=3；（1）求四棱锥A1-ABCD的体积；
（2）求异面直线A1C与DD1所成角的大小．
分析 （1）四棱锥A1-ABCD的体积${V}_{{A}_{1}-ABCD}$=$\frac{1}{3}{S}_{矩形ABCD}×A{A}_{1}$，由此能求出结果．
（2）由DD1∥CC1，知∠A1CC1是异面直线A1C与DD1所成角（或所成角的补角），由此能求出异面直线A1C与DD1所成角的大小．
解答 解：（1）∵长方体ABCD-A1B1C1D1中，AB=BC=2，AA1=3，
∴四棱锥A1-ABCD的体积：
${V}_{{A}_{1}-ABCD}$=$\frac{1}{3}{S}_{矩形ABCD}×A{A}_{1}$=$\frac{1}{3}×AB×AD×A{A}_{1}$=$\frac{1}{3}×2×2×3$=4．
（2）∵DD1∥CC1，∴∠A1CC1是异面直线A1C与DD1所成角（或所成角的补角），
∵tan∠A1CC1=$\frac{{A}_{1}{C}_{1}}{C{C}_{1}}$=$\frac{\sqrt{{2}^{2}+{2}^{2}}}{3}$=$\frac{2\sqrt{2}}{3}$，
∴$∠{A}_{1}C{C}_{1}^{\;}$=$arctan\frac{{2\sqrt{2}}}{3}$．
∴异面直线A1C与DD1所成角的大小为$arctan\frac{{2\sqrt{2}}}{3}$；
点评 本题考查三棱锥的体积的求法，考查异面直线所成角的求法，是中档题，解题时要认真审题，注空间思维能力的培养．
练习册系列答案
相关题目
如图，在△ABC中，$\overrightarrow{BF}=2\overrightarrow{FC}$，$\overrightarrow{AM}=\overrightarrow{MF}=\overrightarrow{FN}$．
17．某同学用“五点法”画函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）在某一周期内的图象时，列表并填入了部分数据，如表：
（Ⅰ）请将上表数据补充完整，并直接写出函数f（x）的解析式；
（Ⅱ）求函数f（x）在区间[-$\frac{π}{2}$，0]上的最大值和最小值．
| ωx+φ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| x | $\frac{π}{3}$ | $\frac{5π}{6}$ | |||
| Asin（ωx+φ） | 0 | $\sqrt{2}$ | -$\sqrt{2}$ | 0 |
（Ⅱ）求函数f（x）在区间[-$\frac{π}{2}$，0]上的最大值和最小值．
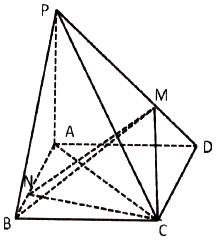如图，四棱锥P-ABCD中，底面ABCD为平行四边形，PA⊥底面ABCD，且PA=AB=AC=2，$BC=2\sqrt{2}$．
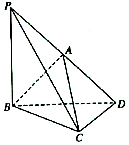如图所示，在三棱锥A-BCD中，A在平面BCD内的投影恰为BD的中点，CD⊥BD，AD⊥AB，延长DA至P，使DA=AP．