题目内容

已知椭圆C：
x2
20
+
y2
15
=1，
（1）若P（x，y）是C上一点，求x+5y的最小值；
（2）证明椭圆C的面积S=10
3
π．
考点：椭圆的简单性质
专题：圆锥曲线的定义、性质与方程
分析：（1）利用椭圆的参数方程、两角和差的正弦公式及其单调性即可得出；
（2）利用椭圆C的面积S=πab即可证明．
解答： （1）解：设x=2
5
cosθ，y=
15
sinθ（θ∈[0，2π）），
则x+5y=2
5
cosθ+5
15
sinθ=
395
sin（θ+φ）≥-
395
，其中φ=arctan
2
3
15
，
∴当sin（θ+φ）=-1时，x+5y取得最小值-
395
．
（2）证明：椭圆C的面积S=πab=π×
20
×
15
=10
3
π．
点评：本题考查了椭圆的参数方程、两角和差的正弦公式及其单调性、椭圆C的面积S=πab，属于中档题．
练习册系列答案
相关题目
已知离心率为
2
2
的椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）过点M(
6
，1)
（1）求椭圆C的方程；
（2）过点（1，0）作斜率为2直线l与椭圆相交于A，B两点，求|AB|的长．
某中学的高二（1）班男同学有45名，女同学有15名，老师按照分层抽样的方法组建了一个4人的课外兴趣小组．
（Ⅰ）求某同学被抽到的概率及课外兴趣小组中男、女同学的人数；
（Ⅱ）经过一个月的学习、讨论，这个兴趣小组决定选出两名同学做某项实验，方法是先从小组里选出1名同学做实验，该同学做完后，再从小组内剩下的同学中选一名同学做实验，求选出的两名同学中恰有一名女同学的概率．
若函数y=3mx2-（2m+6）x+m+3在（-∞，1）上单减，求实数m的取值范围．
已知数列{an}的通项公式an=
1
(n+1)2
（n∈N*），记f（n）=（1-a1）（1-a2）…（1-an）．
（1）试通过计算f（1），f（2），f（3）的值，推测出f（n）的值；
（2）试用数学归纳法证明你的推测．
在△ABC中，角A，B，C的对边分别为a，b，c，且bcosC-ccos（A+C）=3acosB．
（1）求cosB的值；
（2）若
BA
•
BC
=2，且a=
6
，求b的值．
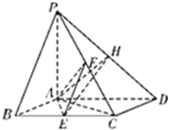如图，已知四棱锥P-ABCD中，底面ABCD为菱形，且AC=AB=BC=2，PA⊥平面ABCD，E，F分别是BC，PC的中点
（1）证明：AE⊥PD；
（2）若H为PD上一点，且AH⊥PD，EH与平面PAD所成角的正切值为
6
2
，求二面角E-AF-C的余弦值．
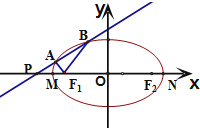已知椭圆E：
x2
a2
+
y2
b2
=1（a＞b＞0）的左焦点为F1（-1，0），且过点Q（1，
2
2
）．
（Ⅰ）求椭圆E的方程； 
（Ⅱ）设过点P（-2，0）的直线与椭圆E交于A、B两点，且满足
BP
=λ
AP
（λ＞1）．
（1）若λ=3，求3|AF1|+|BF1|的值；
（2）若M、N分别为椭圆E的左、右顶点，证明：∠AF1M=∠BF1N．
把正整数按上小下大、左小右大的原则排成如图三角形数表（每行比上一行多一个数）：设ai，j（i、j∈N*）是位于这个三角形数表中从上往下数第i行、从左往右数第j个数，如a4，2=8，则a51，25为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网