题目内容
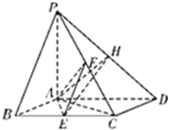 如图,已知四棱锥P-ABCD中,底面ABCD为菱形,且AC=AB=BC=2,PA⊥平面ABCD,E,F分别是BC,PC的中点
如图,已知四棱锥P-ABCD中,底面ABCD为菱形,且AC=AB=BC=2,PA⊥平面ABCD,E,F分别是BC,PC的中点(1)证明:AE⊥PD;
(2)若H为PD上一点,且AH⊥PD,EH与平面PAD所成角的正切值为
| ||
| 2 |
考点:二面角的平面角及求法,直线与平面垂直的性质
专题:空间角
分析:(1)由已知条件推导出△ABC为正三角形,AE⊥BC,AE⊥AD,PA⊥AE,由此能证明AE⊥PD.
(2)由已知条件推导出∠EHA为EH与平面PAD所成的角,由此能求出二面角的余弦值.
(2)由已知条件推导出∠EHA为EH与平面PAD所成的角,由此能求出二面角的余弦值.
解答:
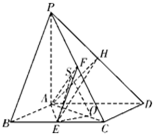 (1)证明:由AC=AB=BC,得△ABC为正三角形.
(1)证明:由AC=AB=BC,得△ABC为正三角形.
因为E为BC的中点,所以AE⊥BC.
又BC∥AD,因此AE⊥AD.
因为PA⊥平面ABCD,AE?平面ABCD,所以PA⊥AE.
而PA?平面PAD,AD?平面PAD且PA∩AD=A,
所以AE⊥平面PAD.又PD?平面PAD,
所以AE⊥PD.(5分)
(2)解:因为AH⊥PD,
由(1)知AE⊥平面PAD,
则∠EHA为EH与平面PAD所成的角.
在Rt△EAH中,AE=
,
此时tan∠EHA=
=
=
,
因此AH=
.又AD=2,所以∠ADH=45°,
所以PA=2.(8分)
因为PA⊥平面ABCD,PA?平面PAC,
所以平面PAC⊥平面ABCD.
过E作EO⊥AC于O,则EO⊥平面PAC,
过O作OS⊥AF于S,连结ES,
则∠ESO为二面角E-AF-C的平面角,
在Rt△AOE中,EO=AE•sin 30°=
,AO=AE•cos 30°=
,
又F是PC的中点,在Rt△ASO中,SO=AO•sin 45°=
,
又SE=
=
=
,
在Rt△ESO中,cos∠ESO=
=
=
,
即所求二面角的余弦值为
.(12分)
 (1)证明:由AC=AB=BC,得△ABC为正三角形.
(1)证明:由AC=AB=BC,得△ABC为正三角形.因为E为BC的中点,所以AE⊥BC.
又BC∥AD,因此AE⊥AD.
因为PA⊥平面ABCD,AE?平面ABCD,所以PA⊥AE.
而PA?平面PAD,AD?平面PAD且PA∩AD=A,
所以AE⊥平面PAD.又PD?平面PAD,
所以AE⊥PD.(5分)
(2)解:因为AH⊥PD,
由(1)知AE⊥平面PAD,
则∠EHA为EH与平面PAD所成的角.
在Rt△EAH中,AE=
| 3 |
此时tan∠EHA=
| AE |
| AH |
| ||
| AH |
| ||
| 2 |
因此AH=
| 2 |
所以PA=2.(8分)
因为PA⊥平面ABCD,PA?平面PAC,
所以平面PAC⊥平面ABCD.
过E作EO⊥AC于O,则EO⊥平面PAC,
过O作OS⊥AF于S,连结ES,
则∠ESO为二面角E-AF-C的平面角,
在Rt△AOE中,EO=AE•sin 30°=
| ||
| 2 |
| 3 |
| 2 |
又F是PC的中点,在Rt△ASO中,SO=AO•sin 45°=
3
| ||
| 4 |
又SE=
| EO2+SO2 |
|
| ||
| 4 |
在Rt△ESO中,cos∠ESO=
| SO |
| SE |
| ||||
|
| ||
| 5 |
即所求二面角的余弦值为
| ||
| 5 |
点评:本题考查异面直线垂直的证明,考查二面角的余弦值的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目