题目内容
已知数列{an}（n∈N+）是各项均为正数且公比不等于1的等比数列，对于函数y=f（x），若数列{lnf（an）}为等差数列，则称函数f（x）为“保比差数列函数”，现有定义在（0，+∞）上的五个数列：
①f（x）=
；②f（x）=ex；③f（x）=
；④y=kx（k＞0）；⑤y=ax2+b（a＞0且b＞0），
则为“保比差数列函数”的是 ．
①f（x）=
| 1 |
| x |
| x |
则为“保比差数列函数”的是
考点：等差数列与等比数列的综合
专题：综合题,等差数列与等比数列
分析：充分运用等比数列的定义，lnf（an）-lnf（an-1）=ln
=d．
=ed=常数，
判断{
=ed}为等比数列，
再分别运用代数运算论证判断，紧扣给定的定义．
| f(an) |
| f(an-1) |
| f(an) |
| f(an-1) |
判断{
| f(an) |
| f(an-1) |
再分别运用代数运算论证判断，紧扣给定的定义．
解答：
解：设数列的公比q，若lnf（an）-lnf（an-1）=ln
=d.
=ed=常数，
∴{
=ed}为等比数列．
①若f（x）=
，则f（an）=
，所以.
=
=
，是等比数列，①为“保比差数列函数”；
②f（x）=ex，.
=e an-an-1不是常数，②不为“保比差数列函数”；
③f（x）=
，.
=
=
=常数，∴{
=ed}为等比数列，③为“保比差数列函数”；
④y=kx（k＞0）；.
=
=q=常数，∴{
=ed}为等比数列．，④为“保比差数列函数”；
⑤y=ax2+b（a＞0且b＞0），.
=
≠常数，∴{
=ed}为等比数列，⑤不为“保比差数列函数”；
故答案为：①③④
| f(an) |
| f(an-1) |
| f(an) |
| f(an-1) |
∴{
| f(an) |
| f(an-1) |
①若f（x）=
| 1 |
| x |
| 1 |
| an |
| f(an) |
| f(an-1) |
| an-1 |
| an |
| 1 |
| q |
②f（x）=ex，.
| f(an) |
| f(an-1) |
③f（x）=
| x |
| f(an) |
| f(an-1) |
| ( ) |
| ( ) |
|
| q |
| f(an) |
| f(an-1) |
④y=kx（k＞0）；.
| f(an) |
| f(an-1) |
| an |
| an-1 |
| f(an) |
| f(an-1) |
⑤y=ax2+b（a＞0且b＞0），.
| f(an) |
| f(an-1) |
| a(an)2+b |
| a(an-1)2+b |
| f(an) |
| f(an-1) |
故答案为：①③④
点评：本题很新颖，融合了阅读分析能力，考查了对等比数列的定义，对数等知识的运用，综合性较强．
练习册系列答案
相关题目
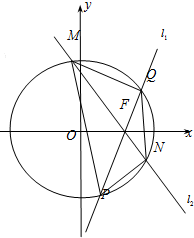已知椭圆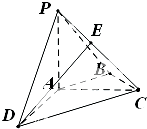
如图，在四棱锥P-ABCD中，PA⊥平面ABCD，AC⊥AD，AB⊥BC，∠BAC=45°，PA=AD=2，AB=
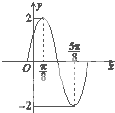已知函数f（x）=Asin（ωx+φ）其中A＞0，ω＞0，0＜φ＜