题目内容
袋中有大小相同的4个红球与2个白球.
(1)若从袋中不放回的依次取出一个球,求第三次取出白球的概率;
(2)若从中有放回的依次取出一个球,记6次取球中取出红球的次数为ξ,求P(ξ≤4)与E(9ξ-1).
(1)若从袋中不放回的依次取出一个球,求第三次取出白球的概率;
(2)若从中有放回的依次取出一个球,记6次取球中取出红球的次数为ξ,求P(ξ≤4)与E(9ξ-1).
考点:离散型随机变量的期望与方差,列举法计算基本事件数及事件发生的概率
专题:概率与统计
分析:(1)第三次取出白球的情况有三种:红红白、红白白,白红白,由此能求出第三次取出白球的概率.
(2)记取一次球取出红球为事件A,则p(A)=
=
,由题意知ξ服从二项分布,即ξ~B(6,
),由此能求出P(ξ≤4)与E(9ξ-1).
(2)记取一次球取出红球为事件A,则p(A)=
| 4 |
| 6 |
| 2 |
| 3 |
| 2 |
| 3 |
解答:
解:(1)∵第三次取出白球的情况有三种:
红红白、红白白,白红白,
∴第三次取出白球的概率:
p=
×
×
+
×
×
+
×
×
=
.
(2)记取一次球取出红球为事件A,则p(A)=
=
,
由题意知ξ服从二项分布,即ξ~B(6,
)
∴p(ξ≤4)=1-p(ξ>4)=1-
(
)5.
-(
)6=
…(9分)
E(9ξ-1)=9Eξ-1=9•6•
-1=35.…(12分)
红红白、红白白,白红白,
∴第三次取出白球的概率:
p=
| 4 |
| 6 |
| 3 |
| 5 |
| 2 |
| 4 |
| 4 |
| 6 |
| 2 |
| 5 |
| 1 |
| 4 |
| 2 |
| 6 |
| 4 |
| 5 |
| 1 |
| 4 |
| 1 |
| 3 |
(2)记取一次球取出红球为事件A,则p(A)=
| 4 |
| 6 |
| 2 |
| 3 |
由题意知ξ服从二项分布,即ξ~B(6,
| 2 |
| 3 |
∴p(ξ≤4)=1-p(ξ>4)=1-
| C | 5 6 |
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 473 |
| 729 |
E(9ξ-1)=9Eξ-1=9•6•
| 2 |
| 3 |
点评:本题考查概率的求法,考查离散型随机变量的数学期望的求法,是中档题,解题时要认真审题,注意二项分布的合理运用.

练习册系列答案
相关题目
已知数列{an}中,a1=
,an+1=
,则a2014=( )
| 4 |
| 5 |
|
A、
| ||
B、
| ||
C、
| ||
D、
|
已知函数f(x)=loga(ax2-x+3)在[2,4]上是增函数,则实数a的取值范围是( )
| A、a>1 | ||||
| B、0<a<1或a>1 | ||||
C、
| ||||
D、
|
已知U={2,3,4,5},M={3,4,5},N={2,4,5},则( )
| A、M∩N={4,3} |
| B、M∪N=U |
| C、{∁UN}∪M=U |
| D、(∁UM)∪N=M |
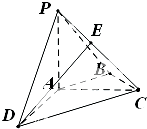 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AC⊥AD,AB⊥BC,∠BAC=45°,PA=AD=2,AB=
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AC⊥AD,AB⊥BC,∠BAC=45°,PA=AD=2,AB=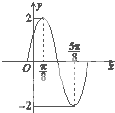 已知函数f(x)=Asin(ωx+φ)其中A>0,ω>0,0<φ<
已知函数f(x)=Asin(ωx+φ)其中A>0,ω>0,0<φ<