题目内容
19．已知f（x）在[-1，1]上既是奇函数又是减函数，则满足f（1-x）+f（3x-2）＜0的x的取值范围是$（{\frac{1}{2}，1}]$．分析 利用函数的奇偶性和单调性，将不等式进行转化，解不等式即可．
解答 解：∵函数y=f（x）在[-1，1]上是奇函数，
∴不等式f（1-x）+f（3x-2）＜0等价为f（1-x）＜-f（3x-2）=f（2-3x）．
又函数在[-1，1]上单调递减，
∴$\left\{\begin{array}{l}{-1≤1-x≤1}\\{-1≤3x-2≤1}\\{1-x＞2-3x}\end{array}\right.$，解得$\frac{1}{2}$＜x≤1．
即不等式成立的x的范围是 $（{\frac{1}{2}，1}]$．
故答案为 $（{\frac{1}{2}，1}]$．
点评 本题主要考查函数奇偶性和单调性的应用，利用条件将函数进行转化是解决本题的关键．
练习册系列答案
相关题目
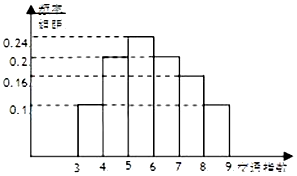交通指数是交通拥堵指数的简称，是综合反映道路网畅通或拥堵的概念，记交通指数为T，其范围为[0，10]，分为五个级别，T∈[0，2）畅通；T∈[2，4）基本畅通；T∈[4，6）轻度拥堵；T∈[6，8）中度拥堵；T∈[8，10]严重拥堵．早高峰时段（T≥3），从某市交通指挥中心随机选取了三环以内的50个交通路段，依据其交通指数数据绘制的频率分布直方图如右图．
14．设$a={（\frac{1}{2}）^{0.7}}$，$b={（\frac{1}{2}）^{0.8}}$，c=log30.7，则（ ）
| A． | c＜b＜a | B． | c＜a＜b | C． | a＜b＜c | D． | b＜a＜c |
4．不等式x2-2|x|-3＜0的解集是（ ）
| A． | （-3，3） | B． | （-3，1） | C． | （-3，0）∪（0，3） | D． | （-1，0）∪（0，1） |