题目内容
函数y=
在x>1的条件下的最小值为 ;此时x= .
| x2-x+4 |
| x-1 |
考点:函数的最值及其几何意义
专题:计算题,不等式的解法及应用
分析:化简y=
=x+
=(x-1)+
+1;注意到x>1,利用基本不等式求最值.
| x2-x+4 |
| x-1 |
| 4 |
| x-1 |
| 4 |
| x-1 |
解答:
解:y=
=x+
=(x-1)+
+1≥4+1=5;
当且仅当x-1=
,x=3时,等号成立.
故答案为:5,3.
| x2-x+4 |
| x-1 |
| 4 |
| x-1 |
=(x-1)+
| 4 |
| x-1 |
当且仅当x-1=
| 4 |
| x-1 |
故答案为:5,3.
点评:本题考查了基本不等式的应用,属于中档题.

练习册系列答案
相关题目
已知圆的方程为x2+y2-6x-8y=0,设该圆内过点 (-3,5)的最长弦和最短弦分别为AC和BD,则四边形ABCD的面积为( )
A、10
| ||
B、20
| ||
C、30
| ||
D、40
|
甲、乙两人同时独立地打靶,谁先打中谁胜(如两人在同一次都打中,则为和局,比赛结束),已知甲命中概率为
,乙命中概率为
,则第二轮分出胜负的概率为( )
| 2 |
| 3 |
| 3 |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
将周期为π的函数y=sin2ωx+2sinωxcosωx-cos2ωx(ω>0)的图象按
=(-
,1)平移后,所得函数图象的解析式为( )
| a |
| π |
| 8 |
A、y=
| ||||
B、y=
| ||||
C、y=
| ||||
D、y=1-
|
函数f(x)=Asin(ωx+ϕ)+k在一个周期内的图象如图,函数f(x)解析式为( )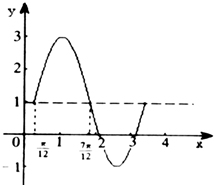

A、f(x)=4sin(
| ||||
B、f(x)=2sin(2x-
| ||||
C、f(x)=4sin(
| ||||
D、f(x)=2sin(2x-
|
在等差数列{an}中,n≥2,公差d<0,前n项和是Sn,则有( )
| A、nan<Sn<na1 |
| B、na1<Sn<nan |
| C、Sn≥na1 |
| D、Sn≤nan |