题目内容
甲、乙两人同时独立地打靶,谁先打中谁胜(如两人在同一次都打中,则为和局,比赛结束),已知甲命中概率为
,乙命中概率为
,则第二轮分出胜负的概率为( )
| 2 |
| 3 |
| 3 |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:相互独立事件的概率乘法公式,互斥事件的概率加法公式
专题:概率与统计
分析:由题意知第一轮只可能两人都没打中,在此前提下第二轮分出胜负的概率是1-
×
-
×
=
,由此能求出第二轮分出胜负的概率.
| 1 |
| 3 |
| 1 |
| 4 |
| 2 |
| 3 |
| 3 |
| 4 |
| 5 |
| 12 |
解答:
解:依据题意,要在第二轮分出胜负,
那么第一轮只可能两人都没打中(否则第一轮就结束了),
这个概率是
+
=
,
在此前提下第二轮分出胜负的概率是:1-
×
-
×
=
,
所以第二轮分出胜负的概率为:
×
=
.
故选:A.
那么第一轮只可能两人都没打中(否则第一轮就结束了),
这个概率是
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 12 |
在此前提下第二轮分出胜负的概率是:1-
| 1 |
| 3 |
| 1 |
| 4 |
| 2 |
| 3 |
| 3 |
| 4 |
| 5 |
| 12 |
所以第二轮分出胜负的概率为:
| 1 |
| 12 |
| 5 |
| 12 |
| 5 |
| 144 |
故选:A.
点评:本题考查概率的求法,是基础题,解题时要认真审题,注意概率乘法公式的合理运用.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案
相关题目
曲线
+
=1与曲线
+
=1(k<9)的( )
| x2 |
| 25 |
| y2 |
| 9 |
| x2 |
| 25-k |
| y2 |
| 9-k |
| A、长轴长相等 | B、短轴长相等 |
| C、离心率相等 | D、焦距相等 |
如图是某同学用于计算S=sin1+sin2+sin3+…+sin2012值的程序框图,则在判断框中填写( )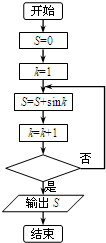

| A、k>2011? |
| B、k>2012? |
| C、k<2011? |
| D、k<2012? |