题目内容
14.函数$f(x)=\frac{ax}{{{x^2}+1}}(a>0)$的单调递增区间是( )| A. | (-∞,-1) | B. | (-1,1) | C. | (1,+∞) | D. | (-∞,-1)∪(1,+∞) |
分析 先对函数求导,然后由y’>0可得x的范围,从而可得函数的单调递增区间.
解答 解:f′(x)=a•$\frac{1{-x}^{2}}{{(1{+x}^{2})}^{2}}$,(a>0),
令f′(x)>0,解得:-1<x<1,
故f(x)在(-1,1)递增,
故选:B.
点评 本题主要考查了函数的导数与函数的单调性关系及应用,导数法是求函数的单调区间的基本方法,一定要熟练掌握.

练习册系列答案
相关题目
4.已知函数f(x)=$\sqrt{2}sinωxcosωx+\sqrt{2}{cos^2}ωx-\frac{{\sqrt{2}}}{2}({ω>0})$,若x=$\frac{π}{4}$是函数f(x)的一条对称轴,则实数ω的值可以是( )
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{8}$ |
5.为了解某地区某种农产品的年产量x(单位:吨)对价格y(单位:千元/吨)和利润z的影响,对近五年该农产品的年产量和价格统计如表:
(Ⅰ)求y关于x的线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$;
(Ⅱ)若每吨该农产品的成本为2千元,假设该农产品可全部卖出,预测当年产量为多少时,年利润z取到最大值?(保留两位小数)
参考公式:$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}({x}_{i}{y}_{i})-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$.
| x | 1 | 2 | 3 | 4 | 5 |
| y | 7.0 | 6.5 | 5.5 | 3.8 | 2.2 |
(Ⅱ)若每吨该农产品的成本为2千元,假设该农产品可全部卖出,预测当年产量为多少时,年利润z取到最大值?(保留两位小数)
参考公式:$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}({x}_{i}{y}_{i})-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$.
19.如图中的网格纸是边长为1的小正方形,在其上用粗线画出了一四棱锥的三视图,则该四棱锥的体积为( )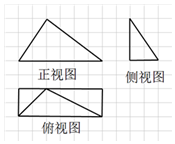

| A. | 12 | B. | 8 | C. | 6 | D. | 4 |
6.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右两个焦点分别为F1、F2,以线段F1F2为直径的圆与双曲线的渐近线在第一象限的交点为M,若|MF1|-|MF2|=2b,该双曲线的离心率为e,则e2=( )
| A. | 2 | B. | $\frac{\sqrt{2}+1}{2}$ | C. | $\frac{3+2\sqrt{2}}{2}$ | D. | $\frac{\sqrt{5}+1}{2}$ |
3.原点与极点重合,x轴正半轴与极轴重合,则点(2,-2$\sqrt{3}$)的极坐标是( )
| A. | (4,$\frac{π}{3}$) | B. | (4,$\frac{4π}{3}$) | C. | (-4,-$\frac{2π}{3}$) | D. | (4,-$\frac{2π}{3}$) |
4.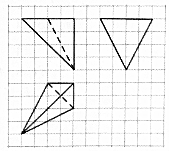 如图,网格纸上小正方形的边长为1,粗线画出的是某三棱锥的三视图,则该三棱锥的体积为( )
如图,网格纸上小正方形的边长为1,粗线画出的是某三棱锥的三视图,则该三棱锥的体积为( )
 如图,网格纸上小正方形的边长为1,粗线画出的是某三棱锥的三视图,则该三棱锥的体积为( )
如图,网格纸上小正方形的边长为1,粗线画出的是某三棱锥的三视图,则该三棱锥的体积为( )| A. | $\frac{8}{3}$ | B. | $\frac{16}{3}$ | C. | $\frac{32}{3}$ | D. | 16 |
