题目内容
在△ABC中,角A,B,C的对边分别为a,b,c,已知acosB+bcosA=2ccosC,
(1)求角C的值;
(2)若△ABC的面积为S=
c,且a+b=2c,求边长c的值.
(1)求角C的值;
(2)若△ABC的面积为S=
| ||
| 4 |
考点:余弦定理的应用,三角函数中的恒等变换应用,正弦定理,余弦定理
专题:解三角形
分析:(1)利用正弦定理把题设中关于边的等式转换成角的正弦,进而利用两角和公式化简整理求得cosC,进而求得C.
(2)根据余弦定理求得a和b的关系式,通过三角形的面积求出abc的关系,结就求出c即可.
(2)根据余弦定理求得a和b的关系式,通过三角形的面积求出abc的关系,结就求出c即可.
解答:
(本题满分14分)
解:(1)由题意得sinAcosB+sinBcosA=2sinCcosC,
即sinC=2sinCcosC,故cosC=
,所以C=
.
(2)△ABC的面积为S=
c=
absinC=
ab,ab=c
cosC=
=
,
所以ab=a2+b2-c2.
由a+b=2c,可得a2+b2+2ab=4c2,即ab=c2,
∴c=1.
解:(1)由题意得sinAcosB+sinBcosA=2sinCcosC,
即sinC=2sinCcosC,故cosC=
| 1 |
| 2 |
| π |
| 3 |
(2)△ABC的面积为S=
| ||
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
cosC=
| 1 |
| 2 |
| a2+b2-c2 |
| 2ab |
所以ab=a2+b2-c2.
由a+b=2c,可得a2+b2+2ab=4c2,即ab=c2,
∴c=1.
点评:本题主要考查了余弦定理的应用,正弦定理的应用,两角和公式的化简求值.综合考查了学生的基础知识的掌握.

练习册系列答案
相关题目
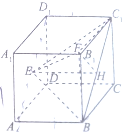 已知正方体ABCD-A1B1C1D1棱长为1,E、F、H分别为面A1ADD1、面DCC1D1与面BCC1B1的中心.
已知正方体ABCD-A1B1C1D1棱长为1,E、F、H分别为面A1ADD1、面DCC1D1与面BCC1B1的中心.