题目内容

16．医院用甲、乙两种原料为手术后的病人配营养餐．甲种原料每10g含5单位蛋白质和10单位铁质，售价3元；乙种原料每10g含7单位蛋白质和4单位铁质，售价2元．若病人每餐至少需要35单位蛋白质和40单位铁质．试问：应如何使用甲、乙原料，才能既满足营养，又使费用最省．

分析 首先由题意，列出两个变量满足的不等式组以及目标函数，然后画出可行域，利用目标函数的几何意义求最值．

解答 解：设甲、乙两种原料分别用10x g和10y g，总费用为z，则$\left\{\begin{array}{l}{5x+7y≥35}\\{10x+4y≥40}\\{x≥0，y≥0}\end{array}\right.$，目标函数为z=3x+2y，作出可行域如图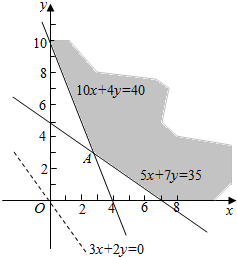

把z=3x+2y变形为y=-$\frac{3}{2}x+\frac{z}{2}$，得到斜率为-$\frac{3}{2}$．在y轴上的截距为$\frac{z}{2}$，随z变化的一族平行直线．
由图可知，当直线y=-$\frac{3}{2}x+\frac{z}{2}$经过可行域上的点A时，截距$\frac{z}{2}$最小，即z最小．
由$\left\{\begin{array}{l}{5x+7y=35}\\{10x+4y=40}\end{array}\right.$得A（$\frac{14}{5}$，3），
∴zmin=3×$\frac{14}{5}$+2×3=14.4．
∴选用甲种原料$\frac{14}{5}$×10=28（g），乙种原料3×10=30（g）时，费用最省．

点评 本题考查了简单线性规划问题的应用；关键是明确题意，列出约束条件，利用数形结合求目标函数的最值．

练习册系列答案
相关题目
6．下列各组函数中，表示同一个函数的是（　　）
A．y=1，y=$\frac{x}{x}$B．y=x，y=$\root{3}{{x}^{3}}$
C．y=$\sqrt{x-1}$×$\sqrt{x+1}$，y=$\sqrt{{x}^{2}-1}$D．y=|x|，$y={（{\sqrt{x}}）^2}$
7．已知p：$\frac{3}{x-1}$≤1，q：x2+x≤a2-a（a＜0），若￢q成立的一个充分而不必要条件是￢p，则实数a的取值范围为（-1，0）．
4．正方体ABCD-A1B1C1D1中，棱长为1，点E，F，G分别是线段AB，BC，DD1的中点，求作过E，F，G三点的截面，并求截面的面积．
11．下列命题中真命题有（1），（5）
（1）已知集合A={1，2}，$B=\left\{{x\left|{x=\frac{1}{a}}\right.}\right\}$，若B⊆A，则a的值为$1或\frac{1}{2}$
（2）已知$f（x）=\left\{\begin{array}{l}（{2-a}）x+1，（{x＜1}）\\{a^x}，（{x≥1}）\end{array}\right.$（a＞0，a≠1）是R上的增函数，那么a的取值范围是（1，2）
（3）函数$f（x）=\frac{1}{x}$在定义域（-∞，0）∪（0，∞）上是减函数
（4）$\left\{{x∈N\left|{\frac{6}{6-x}∈N}\right.}\right\}=\left\{{\frac{6}{6-x}∈N\left|{x∈N}\right.}\right\}$
（5）定义在R上的函数f（x）满足f（x+2）=3f（x），当x∈[0，2]时，f（x）=x2-2x，则x∈[-4，-2]时，f（x）的最小值是$-\frac{1}{9}$．
（6）若A={x|y=x2+1}，B={y|y=x2+1}，C={（x，y）|y=x2+1}，则A∪B=C．
1．以（1，-2）为圆心且过原点的圆的方程为（x-1）2+（y+2）2=5．
8．已知向量$\overrightarrow{a}$=（1，$\sqrt{3}$），$\overrightarrow{b}$=（-2，λ），且$\overrightarrow{a}$与$\overrightarrow{b}$共线，则|$\overrightarrow{a}$+$\overrightarrow{b}$|的值为2．
5．已知a=log0.53，b=20.5，c=0.50.3，则a，b，c三者的大小关系是（　　）
A．b＞a＞cB．b＞c＞aC．a＞b＞cD．c＞b＞a
6．函数f（x）=2log2（x2+1）（x＜-1）的反函数f-1（x）=-$\sqrt{{2}^{\frac{x}{2}}-1}$（x＞2）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网