题目内容
定义在实数集R上的奇函数f(x),对任意实数x都有f(
+x)=f(
-x),且满足f(1)>-2,f(2)=m-
,则实数m的取值范围是( )
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| m |
| A、-1<m<3 |
| B、0<m<3 |
| C、0<m<3或m<-1 |
| D、m>3或m<-1 |
考点:抽象函数及其应用,函数奇偶性的性质
专题:函数的性质及应用
分析:先由题意求出函数为3为周期的周期函数,再根据函数为奇函数得到f(2)<2,代入解不等式即可.
解答:
解:∵f(
+x)=f(
-x),
用x+
代换x得,
∴f(x+
)=f(-x)=-f(x),
再用x+
代换x得,
∴f(x+3)=-f(x+
)=f(x),
∴函数为以3为周期的周期函数,
∴f(x)=-f(-x),f(1)=-f(-1),f(-1)=f(2),
∴-f(2)=-f(-1)=f(1)>-2,
∴f(2)<2,
∴f(2)=m-
<2,
解得0<m<3,或m<-1,
故选:C
| 3 |
| 4 |
| 3 |
| 4 |
用x+
| 3 |
| 4 |
∴f(x+
| 3 |
| 2 |
再用x+
| 3 |
| 2 |
∴f(x+3)=-f(x+
| 3 |
| 2 |
∴函数为以3为周期的周期函数,
∴f(x)=-f(-x),f(1)=-f(-1),f(-1)=f(2),
∴-f(2)=-f(-1)=f(1)>-2,
∴f(2)<2,
∴f(2)=m-
| 3 |
| m |
解得0<m<3,或m<-1,
故选:C
点评:本题考查函数的周期性和奇偶性的应用,解题时要认真审题,仔细解答,属于中档题.

练习册系列答案
相关题目
已知全集U=R,集合M={x|-2≤x<2},P={x|y=
},则M∩(∁UP)等于( )
| x |
| A、[-2,0) |
| B、[-2,0] |
| C、[0,2) |
| D、(0,2) |
i为虚数单位,若
=
,则z等于( )
. |
| z |
| 1+7i |
| 1-i |
| A、-3+4i | B、3+4i |
| C、-3-4i | D、3-4i |
若集合A={x|-2<x<1},B={x|0<x<2},则集合A∩B=( )
| A、{x|0<x<1} |
| B、{x|-1<x<1} |
| C、{x|-2<x<2} |
| D、{x|1<x<2} |
甲乙两人进行围棋比赛,每盘比赛甲胜的概率
,乙胜的概率为
,规定着一人胜3盘则比赛结束,设X为比赛的盘数,则E(X)等于( )
| 1 |
| 3 |
| 2 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
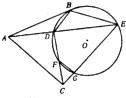 如图,AB是⊙O的切线,B为切点,ADE是⊙O的割线,C是⊙O外一点,且AB=AC,连接BD,BE,CD,CE,CD交⊙O于F,CE交⊙O于G.
如图,AB是⊙O的切线,B为切点,ADE是⊙O的割线,C是⊙O外一点,且AB=AC,连接BD,BE,CD,CE,CD交⊙O于F,CE交⊙O于G.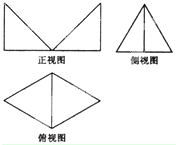 某几何体的三视图如图所示,某正视图是两个全等的三角形,俯视图是一个边长为2的正三角形,俯视图是两个正三角形拼成的菱形,则这个几何体的体积为
某几何体的三视图如图所示,某正视图是两个全等的三角形,俯视图是一个边长为2的正三角形,俯视图是两个正三角形拼成的菱形,则这个几何体的体积为