题目内容
9．三棱柱ABC-A1B1C1中，若三棱锥A1-ABC的体积为9$\sqrt{3}$，则四棱锥A1-B1BCC1的体积为（ ）| A． | $18\sqrt{3}$ | B． | $24\sqrt{3}$ | C． | 18 | D． | 24 |
分析 由题意画出图形，然后利用等积法可得${V}_{{A}_{1}-{B}_{1}BC{C}_{1}}=2{V}_{{A}_{1}-ABC}$，则答案可求．
解答 解：如图，
三棱柱ABC-A1B1C1中，
∵${V}_{{A}_{1}-ABC}={V}_{C-AB{A}_{1}}={V}_{C-{A}_{1}B{B}_{1}}$=${V}_{{A}_{1}-B{B}_{1}C}={V}_{{A}_{1}-{B}_{1}{C}_{1}C}$，
∴${V}_{{A}_{1}-{B}_{1}BC{C}_{1}}=2{V}_{{A}_{1}-ABC}$，
∵三棱锥A1-ABC的体积为9$\sqrt{3}$，则四棱锥A1-B1BCC1的体积为$18\sqrt{3}$．
故选：A．
点评 本题考查棱柱、棱锥、棱台的体积，考查空间想象能力和思维能力，训练了利用等积法求多面体的体积，是中档题．
练习册系列答案
阅读快车系列答案
相关题目
20．
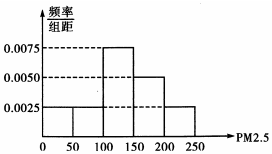PM2.5是衡量空气污染程度的一个指标，为了了解某市空气质量情况，从去年每天的PM2.5值的数据中随机抽取40天的数据，其频率分布直方图如图所示．现将PM2.5的值划分为如下等级
（1）根据样本空气质量PM2.5的数据的频率分布直方图完成下列分布表；
（2）估计该市在下一年的360天中空气质量为一级天气的天数；
（3）在样本中，按照分层抽样的方法从一级天气，三级天气，四级天气的PM2.5值的数据中抽取5天的数据，再从这5个数据中随机抽取2个，求至少一天是一级天气的概率．
PM2.5是衡量空气污染程度的一个指标，为了了解某市空气质量情况，从去年每天的PM2.5值的数据中随机抽取40天的数据，其频率分布直方图如图所示．现将PM2.5的值划分为如下等级| PM2.5 | [0，100） | [100，150） | [150，200） | [200，250] |
| 等级 | 一级 | 二级 | 三级 | 四级 |
| PM2.5 | [0，50） | [50，100） | [100，150） | [150，200） | [200，250] |
| 天数 | 5 | 5 | 15 | 10 | 5 |
（3）在样本中，按照分层抽样的方法从一级天气，三级天气，四级天气的PM2.5值的数据中抽取5天的数据，再从这5个数据中随机抽取2个，求至少一天是一级天气的概率．
20．已知y=lnx+x，x∈[1，e]，则y的最大值为（ ）
| A． | 1 | B． | e-1 | C． | e+1 | D． | e |
4．已知sinα+cosα=-$\frac{1}{5}$，α∈（0，π），则tanα的值为（ ）
| A． | -$\frac{4}{3}$或-$\frac{3}{4}$ | B． | -$\frac{4}{3}$ | C． | -$\frac{3}{4}$ | D． | $\frac{3}{4}$ |