题目内容
1.若点A(ab,a+b)在第一象限内,则直线bx+ay-ab=0不经过第三象限.分析 根据题意,由第一象限点的坐标的特点,分析可得ab>0且a+b>0,即a>0且b>0,然后把直线的方程化为点斜式方程y=kx+b,判断k和b的正负即可得到直线不经过的象限.
解答 解:根据题意,若点A(ab,a+b)在第一象限,
必有ab>0且a+b>0,即a>0且b>0,
直线bx+ay-ab=0,变形可得y=-$\frac{b}{a}$x+b,
又由a>0且b>0,则-$\frac{b}{a}$<0,b>0,
直线bx+ay-ab=0不经过第三象限;
故答案为:三.
点评 本题考查直线的一般式方程,关键由A(ab,a+b)在第一象限内分析a、b的符号.

练习册系列答案
相关题目
9.三棱柱ABC-A1B1C1中,若三棱锥A1-ABC的体积为9$\sqrt{3}$,则四棱锥A1-B1BCC1的体积为( )
| A. | $18\sqrt{3}$ | B. | $24\sqrt{3}$ | C. | 18 | D. | 24 |
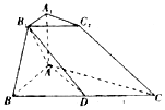 如图所示的三棱台ABC-A1B1C1中,AA1⊥平面ABC,AB⊥BC,AA1=1,AB=2,BC=4,∠ABB1=45°.
如图所示的三棱台ABC-A1B1C1中,AA1⊥平面ABC,AB⊥BC,AA1=1,AB=2,BC=4,∠ABB1=45°.