Question

已知曲线C的方程是（x-

|x|

x

）²+（y-

|y|

y

）²=8，若点P，Q在曲线C上，则|PQ|的最大值是（　　）

• A、6

  2

• B、8

  2

• C、8
• D、6

Answer 1

考点：曲线与方程,两点间距离公式的应用

专题：计算题,直线与圆

分析：先分类讨论化简方程，再根据方程对应的曲线，即可得到结论．

解答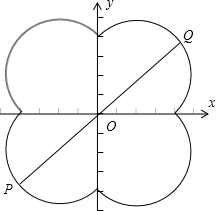： 解：当x＞0，y＞0时，方程是（x-1）²+（y-1）²=8；
当 x＞0，y＜0 时，方程是（x-1）²+（y+1）²=8；
当 x＜0，y＞0 时，方程是（x+1）²+（y-1）²=8；
当 x＜0，y＜0 时，方程是（x+1）²+（y+1）²=8
曲线C既是中心对称图形，又是轴对称图形，对称中心为（0，0），对称轴为x，y轴，点P，Q在曲线C上，当且仅当P，Q与圆弧所在圆心共线时取得最大值，|PQ|的最大值是圆心距加两个半径，即6

2

，
故选：A．

点评：本题考查曲线与方程的概念，体现分类讨论、数形结合的数学思想，属于中档题．