题目内容
12.已知函数f(x)是定义域为R的奇函数,且当x<0时xf'(x)+f(x)<0,记a=3f(3),b=f(sin1)sin1,c=-2$\sqrt{2}f(-2\sqrt{2})$,则a,b,c的大小关系式( )| A. | a>c>b | B. | c>a>b | C. | c>b>a | D. | a>b>c |
分析 令g(x)=xf(x),则g′(x)=f(x)+xf′(x).由于当x<0时xf'(x)+f(x)<0,可得函数g(x)单调递增.即可得出.
解答 解:令g(x)=xf(x),g(x)为偶函数,则g′(x)=f(x)+xf′(x).
∵当x<0时xf'(x)+f(x)<0,
∴当x<0时,函数g(x)单调递减.
∵函数f(x)是定义域为R的奇函数,
∴函数g(x)为R+的单调递增函数,
∴a=3f(3)=g(3),b=sin1•f(sin1)=g(sin1)
c=-2$\sqrt{2}f(-2\sqrt{2})$=g(-2$\sqrt{2}$)=g(2$\sqrt{2}$),
∴g(3)>g(-2$\sqrt{2}$)>g(sin1),
∴a>c>b.
故选:A.
点评 本题考查了通过构造函数利用导数研究函数的单调性比较大小,考查了推理能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
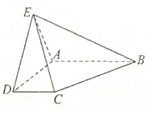 如图,四棱锥E-ABCD中,底面ABCD为梯形,AB∥CD,且AB=2CD,侧面ADE为等边三角形,侧面ABE为等腰直角三角形,且角A为直角,且平面ABE⊥平面ADE.
如图,四棱锥E-ABCD中,底面ABCD为梯形,AB∥CD,且AB=2CD,侧面ADE为等边三角形,侧面ABE为等腰直角三角形,且角A为直角,且平面ABE⊥平面ADE.