题目内容
设x＞0，y＞0且2x+5y=200，则lgx+lgy最大值是 ．
考点：对数的运算性质
专题：函数的性质及应用
分析：由已知得xy≤1000，从而求出lgx+lgy=lg（xy）≤lg1000=3．由此得到lgx+lgy最大值是3．
解答：
解：∵x＞0，y＞0，且2x+5y=200，
∴10xy≤（
）2=10000，
∴xy≤1000，
∴lgx+lgy=lg（xy）≤lg1000=3．
∴lgx+lgy最大值是3．
故答案为：3．
∴10xy≤（
| 200 |
| 2 |
∴xy≤1000，
∴lgx+lgy=lg（xy）≤lg1000=3．
∴lgx+lgy最大值是3．
故答案为：3．
点评：本题考查函数的最大值的求法，是基础题，解题时要认真审题，注意对数性质和运算法则的合理运用．
练习册系列答案
相关题目
设全集U=Z，P={1，2，3，4}，Q={-1，2}，则Q∩∁UP=（ ）
| A、{2} |
| B、{-1} |
| C、{-1，2} |
| D、{1，3，4} |
某程序图如图所示，该程序运行后输出的结果是（ ）
| A、3 | B、4 | C、5 | D、6 |
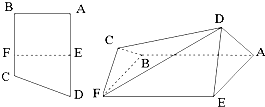如图：直角梯形ABCD中，AD∥BC，∠ABC=90°，E，F分别为边AD和BC上的点，且EF∥AB，AD=2AE=2AB=4FC=4，将四边形EFCD沿EF折起成如图的位置，使AD=AE．