题目内容
13.求满足下列条件的椭圆的标准方程.(1)焦点在y轴上,c=6,$e=\frac{2}{3}$;
(2)短轴的一个端点到一个焦点的距离为5,焦点到椭圆中心的距离为3.
分析 (1)利用椭圆的离心率,求出a,b即可得到椭圆方程.
(2)利用已知条件列出方程,求出a,b,即可求出椭圆方程.
解答 (本题满分10分)
解:(1)焦点在y轴上,c=6,$e=\frac{2}{3}$;
可得$\frac{6}{a}$=$\frac{2}{3}$,所以a=9,则b=$\sqrt{{a}^{2}-{c}^{2}}$=$\sqrt{45}$.
所求椭圆方程为:$\frac{y^2}{81}+\frac{x^2}{45}=1$.…(5分)
(2)解:由题意知,a=5,c=3,
所以b2=a2-c2=25-9=16,…(6分)
若焦点在x轴上,则椭圆的标准方程为$\frac{x^2}{25}+\frac{y^2}{16}=1$,…(8分)
若焦点在y轴上,则椭圆的标准方程为$\frac{y^2}{25}+\frac{x^2}{16}=1$.…(10分)
点评 本题考查椭圆的简单性质的应用,椭圆方程的求法,考查转化思想以及计算能力.

练习册系列答案
相关题目
4.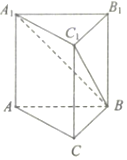 《九章九术》是我国古代数学名著,它在几何学中的研究比西方早一千多年.例如堑堵指底面为直角三角形,且侧棱垂直于底面的三棱柱;阳马指底面为矩形,一侧棱垂直于底面的四棱锥.如图,在堑堵ABC-A1B1C1中,AC⊥BC,若A1A=AB=2,当阳马B-A1ACC1体积最大时,则堑堵ABC-A1B1C1的体积为( )
《九章九术》是我国古代数学名著,它在几何学中的研究比西方早一千多年.例如堑堵指底面为直角三角形,且侧棱垂直于底面的三棱柱;阳马指底面为矩形,一侧棱垂直于底面的四棱锥.如图,在堑堵ABC-A1B1C1中,AC⊥BC,若A1A=AB=2,当阳马B-A1ACC1体积最大时,则堑堵ABC-A1B1C1的体积为( )
 《九章九术》是我国古代数学名著,它在几何学中的研究比西方早一千多年.例如堑堵指底面为直角三角形,且侧棱垂直于底面的三棱柱;阳马指底面为矩形,一侧棱垂直于底面的四棱锥.如图,在堑堵ABC-A1B1C1中,AC⊥BC,若A1A=AB=2,当阳马B-A1ACC1体积最大时,则堑堵ABC-A1B1C1的体积为( )
《九章九术》是我国古代数学名著,它在几何学中的研究比西方早一千多年.例如堑堵指底面为直角三角形,且侧棱垂直于底面的三棱柱;阳马指底面为矩形,一侧棱垂直于底面的四棱锥.如图,在堑堵ABC-A1B1C1中,AC⊥BC,若A1A=AB=2,当阳马B-A1ACC1体积最大时,则堑堵ABC-A1B1C1的体积为( )| A. | $\frac{8}{3}$ | B. | $\sqrt{2}$ | C. | 2 | D. | $2\sqrt{2}$ |
1.已知空间两点A(3,3,1),B(-1,1,5),则线段AB的长度为( )
| A. | 6 | B. | $2\sqrt{6}$ | C. | $4\sqrt{3}$ | D. | $2\sqrt{14}$ |
18.阅读如图的程序框图,运行相应的程序,则输出的T的值为( )


| A. | 57 | B. | 120 | C. | 183 | D. | 247 |
2.若命题“p∧(¬q)”与“¬p”均为假命题,则( )
| A. | p真q真 | B. | p假q真 | C. | p假q假 | D. | p真q假 |
15.设随机变量ξ等可能取值1,2,3,4,…,n,如果p(ξ<4)=0.3,则n的值为( )
| A. | 3 | B. | 4 | C. | 10 | D. | 不能确定 |