题目内容
12．如图，已知四边形ABCD的直观图是一个边长为1的正方形，则原图形的面积为（ ）
| A． | $2\sqrt{2}$ | B． | 6 | C． | 8 | D． | 4$\sqrt{2}$+2 |
分析 根据四边形ABCD的直观图是一个边长为1的正方形，可得原图形为平行四边形，一组对边长为1，高为2$\sqrt{2}$，即可求出原图形的面积．
解答 解：∵四边形ABCD的直观图是一个边长为1的正方形，
∴原图形为平行四边形，一组对边长为1，高为2$\sqrt{2}$，
∴原图形的面积为2$\sqrt{2}$．
故选：A．
点评 本题考查的知识点是平面图形的直观图，其中斜二测画法的规则，能够帮助我们快速的在直观图面积和原图面积之间进行转化．
练习册系列答案
相关题目
9．
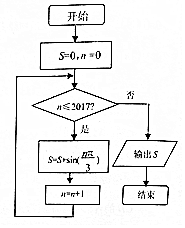执行如图所示的程序框图，则输出S的值为（ ）
执行如图所示的程序框图，则输出S的值为（ ）| A． | $\frac{\sqrt{3}}{2}$ | B． | -$\frac{\sqrt{3}}{2}$ | C． | 0 | D． | $\frac{1}{2}$ |
7．下列命题中，真命题是（ ）
| A． | ?x∈R，2x＞x2 | B． | ?x∈R，ex＜0 | ||
| C． | 若a＞b，c＞d，则a-c＞b-d | D． | ac2＞bc2是a＞b的充分不必要条件 |
4．已知双曲线C1：$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（{a＞0，b＞0}）$一焦点与抛物线y2=8x的焦点F相同，若抛物线y2=8x的焦点到双曲线C1的渐近线的距离为1，P为双曲线左支上一动点，Q（1，3），则|PF|+|PQ|的最小值为（ ）
| A． | 4$\sqrt{2}$ | B． | 4$\sqrt{3}$ | C． | 4 | D． | 2$\sqrt{3}+3\sqrt{2}$ |