题目内容
18.已知函数f(x)=|x-3|-2|x+1|的最大值为m.(1)求m的值和不等式f(x)<1的解集;
(2)若a,b∈(0,+∞),a2+2b2+c2=m,求ab+bc的最大值.
分析 (1)分类讨论,求出函数的值域,即可求m的值;
( 2)由(1)知,a2+2b2+c2=4,利用基本不等式求ab+bc的最大值.
解答 解:(1)当x≤-1时,f(x)=(3-x)+2(x+1)=x+5≤4;
当-1<x<3时,f(x)=(3-x)-2(x+1)=-3x+1∈(-8,4);
当x≥3时,f(x)=(x-3)-2(x+1)=-x-5≤-8.…(3分)
故当x=-1时,f(x)取得最大值m=4;
|x-3|-2|x+1|<1,可化为
当x≤-1时,x+5<1,∴x<-4;当-1<x<3时,-3x+1<1,∴x>0,∴0<x<3;
当x≥3时,-x-5<1,∴x>-4,∴x≥3,
综上所述,不等式f(x)<1的解集为{x|x<-4或x>0};
(2)由(2)知,a2+2b2+c2=4,则ab+bc≤$\frac{1}{2}$[(a2+b2)+(b2+c2)]=2,
∴ab+bc的最大值为2.
点评 本题考查绝对值不等式,考查基本不等式的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
9.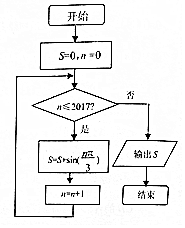 执行如图所示的程序框图,则输出S的值为( )
执行如图所示的程序框图,则输出S的值为( )
 执行如图所示的程序框图,则输出S的值为( )
执行如图所示的程序框图,则输出S的值为( )| A. | $\frac{\sqrt{3}}{2}$ | B. | -$\frac{\sqrt{3}}{2}$ | C. | 0 | D. | $\frac{1}{2}$ |
6.(x2+3x-y)5的展开式中,x5y2的系数为( )
| A. | -90 | B. | -30 | C. | 30 | D. | 90 |
13.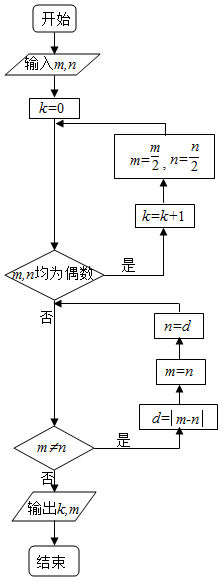 执行如图所示的程序框图,如果输入的m=168,n=112,则输出的k,m的值分别为( )
执行如图所示的程序框图,如果输入的m=168,n=112,则输出的k,m的值分别为( )
 执行如图所示的程序框图,如果输入的m=168,n=112,则输出的k,m的值分别为( )
执行如图所示的程序框图,如果输入的m=168,n=112,则输出的k,m的值分别为( )| A. | 4,7 | B. | 4,56 | C. | 3,7 | D. | 3,56 |
3.已知函数f(x)=$\sqrt{2}$sinωx+$\sqrt{2}$cosωx(ω>0),在区间(-$\frac{π}{3}$,$\frac{π}{4}$)上单调递增,则ω的取值范围为( )
| A. | (0,1] | B. | [1,2) | C. | [$\frac{1}{3}$,2) | D. | (2,+∞) |
7.下列命题中,真命题是( )
| A. | ?x∈R,2x>x2 | B. | ?x∈R,ex<0 | ||
| C. | 若a>b,c>d,则a-c>b-d | D. | ac2>bc2是a>b的充分不必要条件 |