题目内容
在△ABC中，已知a=8，∠B=60°，∠C=75°，则b等于 ．
考点：正弦定理
专题：计算题,解三角形
分析：由B与C的度数求出A的度数，确定出sinA与sinB的值，再由a的值，利用正弦定理即可求出b的值．
解答：
解：∵a=8，B=60°，C=75°，即A=45°，
∴由正弦定理
=
，
得：b=
=
=4
．
故答案为：4
∴由正弦定理
| a |
| sinA |
| b |
| sinB |
得：b=
| asinB |
| sinA |
| 8×sin60° |
| sin45° |
| 6 |
故答案为：4
| 6 |
点评：此题考查了正弦定理，以及特殊角的三角函数值，熟练掌握定理是解本题的关键．
练习册系列答案
黄冈创优卷系列答案
相关题目
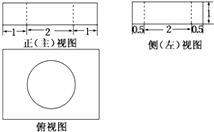
如图是某几何体的三视图，则该几何体的表面积是（ ）
| A、π | ||
B、
| ||
C、
| ||
| D、4π |
一个平面截一个球得到截面面积为16πcm2的圆面，球心到这个平面的距离是3cm，则该球的表面积是（ ）
| A、16πcm2 |
| B、25πcm2 |
| C、75πcm2 |
| D、100πcm2 |