题目内容
若两直线x+y+5a=0与x-y-a=0的交点在曲线y=x2+a上，则a= ．
考点：两条直线的交点坐标
专题：直线与圆
分析：联立
，解得交点．由于两直线x+y+5a=0与x-y-a=0的交点在曲线y=x2+a上，把交点坐标代入即可解出．
|
解答：
解：联立
，解得
．
∵两直线x+y+5a=0与x-y-a=0的交点在曲线y=x2+a上，
∴-3a=（-2a）2+a，化为a（a+1）=0，
解得a=0或-1．
故答案为：0或-1．
|
|
∵两直线x+y+5a=0与x-y-a=0的交点在曲线y=x2+a上，
∴-3a=（-2a）2+a，化为a（a+1）=0，
解得a=0或-1．
故答案为：0或-1．
点评：本题考查了两条直线的交点、一元二次方程的解法，属于基础题．
练习册系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
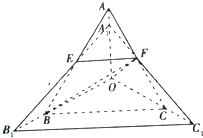如图，在三棱锥A-BOC中，OA，OB，OC两两垂直，OA=OB=OC=2，E，F分别是棱AB，AC的中点．