题目内容
设f(x)=2x3+ax2+bx+1的导数为f′(x),若函数y=f′(x)的图象关于直线x=-
对称,且函数f(x)在x=1处取得极值.
(I)求实数a,b的值;
(Ⅱ)求函数f(x)的单调区间.
| 1 |
| 2 |
(I)求实数a,b的值;
(Ⅱ)求函数f(x)的单调区间.
考点:利用导数研究函数的单调性
专题:导数的综合应用
分析:(Ⅰ)先对f(x)求导,f(x)的导数为二次函数,由对称性可求得a,再由f′(1)=0即可求出b,
(Ⅱ)对f(x)求导,分别令f′(x)大于0和小于0,即可解出f(x)的单调区间.
(Ⅱ)对f(x)求导,分别令f′(x)大于0和小于0,即可解出f(x)的单调区间.
解答:
( I)求导得:f'(x)=6x2+2ax+b
依题意有:
,
解得:a=3,b=-12
( II)由( I)可得:f'(x)=6x2+6x-12=6(x-1)(x+2)
令f'(x)>0得:x>1或x<-2
令f'(x)<0得:-2<x<1
综上:函数f(x)的单调递增区间是(-∞,-2),(1,+∞),单调递减区间是(-2,1)
依题意有:
|
解得:a=3,b=-12
( II)由( I)可得:f'(x)=6x2+6x-12=6(x-1)(x+2)
令f'(x)>0得:x>1或x<-2
令f'(x)<0得:-2<x<1
综上:函数f(x)的单调递增区间是(-∞,-2),(1,+∞),单调递减区间是(-2,1)
点评:本题考查函数的对称性、函数的单调区间和极值,考查运算能力.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目
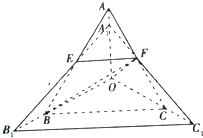 如图,在三棱锥A-BOC中,OA,OB,OC两两垂直,OA=OB=OC=2,E,F分别是棱AB,AC的中点.
如图,在三棱锥A-BOC中,OA,OB,OC两两垂直,OA=OB=OC=2,E,F分别是棱AB,AC的中点.