题目内容
20.曲线y=(x+1)ex在点(0,1)处的切线方程为y=2x+1.分析 求出导函数y′,根据导数的几何意义求出切线的斜率,由直线方程的点斜式即可求出切线方程.
解答 解:∵y=(x+1)•ex(e为自然对数的底数),
∴y′=(x+2)ex,
根据导数的几何意义,则切线的斜率为y′|x=0=2,
又切点坐标为(0,1),
由点斜式方程可得y=2x+1,
∴曲线y=(x+1)•ex(e为自然对数的底数)在点(0,1)处的切线方程为y=2x+1.
故答案为:y=2x+1.
点评 本题考查了利用导数研究曲线上某点切线方程.导数的几何意义即在某点处的导数即该点处切线的斜率,解题时要注意运用切点在曲线上和切点在切线上.属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.下列赋值语句正确的是( )
| A. | 2=x | B. | x=y=z | C. | y=x+1 | D. | x+y=z |
19.正方体ABCD-A1B1C1D1中,与对角线A1B成45°的棱有( )条.
| A. | 4 | B. | 8 | C. | 12 | D. | 2 |
 交通指数是交通拥堵指数的简称,是综合反映道路网畅通或拥堵的概念,记交通指数为T,其范围分为五个级别,T∈[0,2)畅通;T∈[2,4)基本畅通; T∈[4,6)轻度拥堵;T∈[6,8)中度拥堵;T∈[8,10]严重拥堵.早高峰时段(T≥3),从某市交通指挥中心随机选取了三环以内的50个交通路段,依据其交通指数数据绘制的频率分布直方图如图.
交通指数是交通拥堵指数的简称,是综合反映道路网畅通或拥堵的概念,记交通指数为T,其范围分为五个级别,T∈[0,2)畅通;T∈[2,4)基本畅通; T∈[4,6)轻度拥堵;T∈[6,8)中度拥堵;T∈[8,10]严重拥堵.早高峰时段(T≥3),从某市交通指挥中心随机选取了三环以内的50个交通路段,依据其交通指数数据绘制的频率分布直方图如图.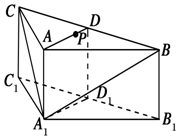 如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB=AC,D,D1分别是线段BC,B1C1的中点,P是线段AD上异于端点的点.
如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB=AC,D,D1分别是线段BC,B1C1的中点,P是线段AD上异于端点的点.