题目内容
某程序框图如图所示，现输入如下四个函数，则可以输出的函数是（ ）
| A、f（x）=xex | ||
B、f（x）=
| ||
C、f（x）=
| ||
| D、f（x）=x3sinx |
考点：程序框图
专题：算法和程序框图
分析：根据程序框图可知函数满足两个条件，一是函数是奇函数，二是函数存在零点，分别进行判断即可．
解答：
解：若满足条件f（x）+f（-x）=0，即f（-x）=-f（x），则函数为奇函数，
若f（x）=xex，则函数f（x）为非奇非偶函数，不满足条件．
若f（x）=
，则f（-x）=-
=-f（x）为奇函数，满足第一个条件，由f（x）=
=0，解得x=0，满足第二个条件．
若f（x）=
，则f（-x）=-f（x），满足第一个条件，由f（x）=0得x=0，此时分母无意义，∴f（x）不存在零点．
若f（x）=x3sinx，则f（x）是偶函数，不满足第一个条件，
故选：B．
若f（x）=xex，则函数f（x）为非奇非偶函数，不满足条件．
若f（x）=
| ex-e-x |
| ex+e-x |
| ex-e-x |
| ex+e-x |
| ex-e-x |
| ex+e-x |
若f（x）=
| |x| |
| x |
若f（x）=x3sinx，则f（x）是偶函数，不满足第一个条件，
故选：B．
点评：本题主要考查程序框图的识别和应用，根据程序满足的条件是解决本题的关键．
练习册系列答案
相关题目
设直线l1：2x-my-1=0，l2：（m-1）x-y+1=0．则“m=2”是“l1∥l2”的（ ）
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
设全集U=R，集合A={x|x2-1＜0}，B={x|x（x-2）≥0}，则A∩（∁UB）=（ ）
| A、{x|0＜x＜2} |
| B、{x|0＜x＜1} |
| C、{x|0≤x＜1} |
| D、{x|-1＜x＜0} |
下列函数中既是奇函数，又在区间[-1，1]上单调递减的函数是（ ）
| A、f（x）=|tan2x| | ||||||
| B、f（x）=-|x+1| | ||||||
C、f（x）=
| ||||||
D、f（x）=log
|
已知ω＞0，|φ|＜| π |
| 2 |
A、向右平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向左平移
|
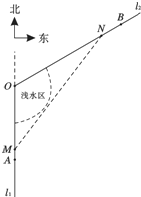某港湾的平面示意图如图所示，O，A，B分别是海岸线l1，l2上的三个集镇，A位于O的正南方向6km处，B位于O的北偏东60°方向10km处．