题目内容
17.已知数列{an}的前n项和为Sn,且Sn=$\frac{1}{2}$n2+$\frac{1}{2}$n,则$\frac{1}{{a}_{1}{a}_{2}}$+$\frac{1}{{a}_{2}{a}_{3}}$+…+$\frac{1}{{a}_{n}{a}_{n+1}}$=$\frac{n}{n+1}$.分析 利用递推关系与“裂项求和”即可得出.
解答 解:∵Sn=$\frac{1}{2}$n2+$\frac{1}{2}$n,∴当n=1时,a1=S1=1;当n≥2时,an=Sn-Sn-1=$\frac{1}{2}$n2+$\frac{1}{2}$n-$[\frac{1}{2}(n-1)^{2}+\frac{1}{2}(n-1)]$,化为an=n.
∴$\frac{1}{{a}_{n}{a}_{n+1}}$=$\frac{1}{n(n+1)}$=$\frac{1}{n}-\frac{1}{n+1}$.
则$\frac{1}{{a}_{1}{a}_{2}}$+$\frac{1}{{a}_{2}{a}_{3}}$+…+$\frac{1}{{a}_{n}{a}_{n+1}}$=$(1-\frac{1}{2})+(\frac{1}{2}-\frac{1}{3})$+…+$(\frac{1}{n}-\frac{1}{n+1})$=1-$\frac{1}{n+1}$=$\frac{n}{n+1}$.
故答案为:$\frac{n}{n+1}$.
点评 本题考查了递推关系与“裂项求和”方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.定义在R的奇函数f(x),当x∈(-∞,0)时,f(x)+xf′(x)<0恒成立,若a=(log3π)•f(log3π),b=(logπ3)•f(logπ3),c=(-lnπ)•f(-lnπ),则( )
| A. | c>a>b | B. | c>b>a | C. | a>c>b | D. | a>b>c |
 已知圆锥的底面半径为3,母线长为5,在圆锥内部放置一个内接圆柱(圆柱的一底面与圆锥的底面重合),
已知圆锥的底面半径为3,母线长为5,在圆锥内部放置一个内接圆柱(圆柱的一底面与圆锥的底面重合),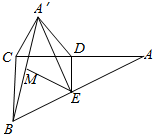 已知在△ABC中,D,E分别为AC,AB的中点,沿DE将△ADE折起,使A到A′的位置,若M是A′B的中点,求证:ME∥平面A′CD.
已知在△ABC中,D,E分别为AC,AB的中点,沿DE将△ADE折起,使A到A′的位置,若M是A′B的中点,求证:ME∥平面A′CD. 如图,ABCD是边长为2的正方形,ED=1,DE⊥平面ABCD,EF∥BD,且EF=$\frac{1}{2}$BD.
如图,ABCD是边长为2的正方形,ED=1,DE⊥平面ABCD,EF∥BD,且EF=$\frac{1}{2}$BD.