题目内容
18.已知集合A={x|(x-3)(x+1)≤0},B={x|-2<x≤2},则A∩B=( )| A. | [-2,-1] | B. | [-1,2] | C. | [-1,1] | D. | [1,2] |
分析 根据题意和交集的运算直接求出A∩B.
解答 解:因为A={x|(x-3)(x+1)≤0}=[-1,3],B={x|-2<x≤2}=(-2,2],
所以A∩B=[-1,2],
故选:B.
点评 本题考查交集及其运算,以及利用不等式的解法,属于基础题.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案
相关题目
10.某研究小组在电脑上进行人工降雨模拟实验,准备用A、B、C三种人工降雨方式分别对甲,乙,丙三地实施人工降雨,其实验统计结果如下
假定对甲、乙、丙三地实施的人工降雨彼此互不影响,且不考虑洪涝灾害,请根据统计数据:
(Ⅰ)求甲、乙、丙三地都恰为中雨的概率;
(Ⅱ)考虑不同地区的干旱程度,当雨量达到理想状态时,能缓解旱情,若甲、丙地需中雨即达到理想状态,乙地必须是大雨才达到理想状态,记“甲,乙,丙三地中缓解旱情的个数”为随机变量X,求X的分布列和数学期望.
| 方式 | 实施地点 | 大雨 | 中雨 | 小雨 | 模拟实验次数 |
| A | 甲 | 2次 | 6次 | 4次 | 12次 |
| B | 乙 | 3次 | 6次 | 3次 | 12次 |
| C | 丙 | 2次 | 2次 | 8次 | 12次 |
(Ⅰ)求甲、乙、丙三地都恰为中雨的概率;
(Ⅱ)考虑不同地区的干旱程度,当雨量达到理想状态时,能缓解旱情,若甲、丙地需中雨即达到理想状态,乙地必须是大雨才达到理想状态,记“甲,乙,丙三地中缓解旱情的个数”为随机变量X,求X的分布列和数学期望.
13. 一光源P在桌面A的正上方,半径为2的球与桌面相切,且PA与球相切,小球在光源P的中心投影下在桌面产生的投影为一椭圆,如图所示,形成一个空间几何体,且正视图是Rt△PAB,其中PA=6,则该椭圆的短轴长为( )
一光源P在桌面A的正上方,半径为2的球与桌面相切,且PA与球相切,小球在光源P的中心投影下在桌面产生的投影为一椭圆,如图所示,形成一个空间几何体,且正视图是Rt△PAB,其中PA=6,则该椭圆的短轴长为( )
 一光源P在桌面A的正上方,半径为2的球与桌面相切,且PA与球相切,小球在光源P的中心投影下在桌面产生的投影为一椭圆,如图所示,形成一个空间几何体,且正视图是Rt△PAB,其中PA=6,则该椭圆的短轴长为( )
一光源P在桌面A的正上方,半径为2的球与桌面相切,且PA与球相切,小球在光源P的中心投影下在桌面产生的投影为一椭圆,如图所示,形成一个空间几何体,且正视图是Rt△PAB,其中PA=6,则该椭圆的短轴长为( )| A. | 6 | B. | 8 | C. | $4\sqrt{3}$ | D. | 3 |
10.执行如图所示的程序框图,如果输出的结果为0,那么输入的x为( )


| A. | $\frac{1}{9}$ | B. | -1或1 | C. | 1 | D. | -1 |
8.按如图所示的程序框图,若输入a=81,则输出的i=( )
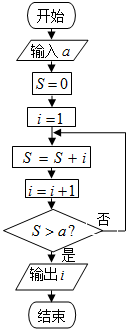

| A. | 14 | B. | 17 | C. | 19 | D. | 21 |
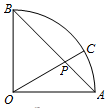 如图,扇形AOB的圆心角为90°,点P在弦AB上,且OP=$\sqrt{2}$AP,延长OP交弧AB于点C,现向该扇形内随机投一点,则该点落在扇形AOC内的概率为$\frac{1}{3}$.
如图,扇形AOB的圆心角为90°,点P在弦AB上,且OP=$\sqrt{2}$AP,延长OP交弧AB于点C,现向该扇形内随机投一点,则该点落在扇形AOC内的概率为$\frac{1}{3}$.