题目内容
14.已知函数f(x)=|x-1|,不等式f(x+5)≤3m(m>0)的解集为[-7,-1](1)求m的值;
(2)已知a>0,b>0,且2a2+b2=3m,求2a$\sqrt{1+{b}^{2}}$的最大值.
分析 (1)解绝对值不等式求得它的解集为[-4-3m,3m-4],再根据它的解集为[-7,-1],可得$\left\{\begin{array}{l}{-4-3m=-7}\\{3m-4=-1}\end{array}\right.$,从而求得 m的值.
(2)根据2a$\sqrt{1+{b}^{2}}$=$\sqrt{2}$•$\sqrt{2}$a•$\sqrt{1{+b}^{2}}$,利用基本不等式求得它的最大值.
解答 解:(1)函数f(x)=|x-1|,不等式f(x+5)≤3m(m>0),即|x+4|≤3m,即-3m≤x+4≤3m,
即-4-3m≤x≤3m-4,即不等式的解集为[-4-3m,3m-4].
再根据它的解集为[-7,-1],可得$\left\{\begin{array}{l}{-4-3m=-7}\\{3m-4=-1}\end{array}\right.$,∴m=1.
(2)已知a>0,b>0,且2a2+b2=3m=3,∴2a$\sqrt{1+{b}^{2}}$=$\sqrt{2}$•$\sqrt{2}$a•$\sqrt{1{+b}^{2}}$≤$\sqrt{2}$•$\frac{{2a}^{2}+1{+b}^{2}}{2}$=2$\sqrt{2}$,
当且仅当$\sqrt{2}$a=$\sqrt{1{+b}^{2}}$ 时,即a=b=1时,等号成立,故2a$\sqrt{1+{b}^{2}}$的最大值为2$\sqrt{2}$.
点评 本题主要考查绝对值不等式的解法,基本不等式的应用,属于中档题.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
5.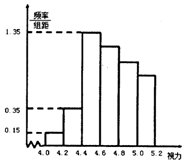 某校高一共录取新生1000名,为了解学生视力情况,校医随机抽取了100名学生进行视力测试,并得到如下频率分布直方图.
某校高一共录取新生1000名,为了解学生视力情况,校医随机抽取了100名学生进行视力测试,并得到如下频率分布直方图.
(Ⅰ)若视力在4.6~4.8的学生有24人,试估计高一新生视力在4.8以上的人数;
(Ⅱ)校医发现学习成绩较高的学生近视率较高,又在抽取的100名学生中,对成绩在前50名的学生和其他学生分别进行统计,得到如右数据,根据这些数据,校医能否有超过95%的把握认为近视与学习成绩有关?
(Ⅲ)用分层抽样的方法从(Ⅱ)中27名不近视的学生中抽出6人,再从这6人中任抽2人,其中抽到成绩在前50名的学生人数为ξ,求ξ的分布列和数学期望.
附:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
 某校高一共录取新生1000名,为了解学生视力情况,校医随机抽取了100名学生进行视力测试,并得到如下频率分布直方图.
某校高一共录取新生1000名,为了解学生视力情况,校医随机抽取了100名学生进行视力测试,并得到如下频率分布直方图.(Ⅰ)若视力在4.6~4.8的学生有24人,试估计高一新生视力在4.8以上的人数;
| 1~50名 | 951~1000名 | |
| 近视 | 41 | 32 |
| 不近视 | 9 | 18 |
(Ⅲ)用分层抽样的方法从(Ⅱ)中27名不近视的学生中抽出6人,再从这6人中任抽2人,其中抽到成绩在前50名的学生人数为ξ,求ξ的分布列和数学期望.
附:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
| P(K2≥k) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
19.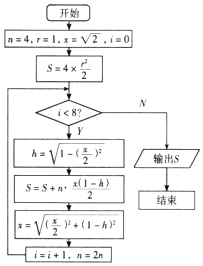 我国魏晋时期的数学家刘徽,他在注《九章算术》中采用正多边形面积逐渐逼近圆面积的算法计算圆周率π,用刘徽自己的原话就是“割之弥细,所失弥少,割之又割,以至于不可割,则与圆合体而无所失矣.”设计程序框图是计算圆周率率不足近似值的算法,其中圆的半径为1.请问程序中输出的S是圆的内接正( )边形的面积.
我国魏晋时期的数学家刘徽,他在注《九章算术》中采用正多边形面积逐渐逼近圆面积的算法计算圆周率π,用刘徽自己的原话就是“割之弥细,所失弥少,割之又割,以至于不可割,则与圆合体而无所失矣.”设计程序框图是计算圆周率率不足近似值的算法,其中圆的半径为1.请问程序中输出的S是圆的内接正( )边形的面积.
 我国魏晋时期的数学家刘徽,他在注《九章算术》中采用正多边形面积逐渐逼近圆面积的算法计算圆周率π,用刘徽自己的原话就是“割之弥细,所失弥少,割之又割,以至于不可割,则与圆合体而无所失矣.”设计程序框图是计算圆周率率不足近似值的算法,其中圆的半径为1.请问程序中输出的S是圆的内接正( )边形的面积.
我国魏晋时期的数学家刘徽,他在注《九章算术》中采用正多边形面积逐渐逼近圆面积的算法计算圆周率π,用刘徽自己的原话就是“割之弥细,所失弥少,割之又割,以至于不可割,则与圆合体而无所失矣.”设计程序框图是计算圆周率率不足近似值的算法,其中圆的半径为1.请问程序中输出的S是圆的内接正( )边形的面积.| A. | 1024 | B. | 2048 | C. | 3072 | D. | 1536 |
6.已知$\frac{1-ai}{1+i}=b-i$(a,b∈R),其中i为虚数单位,则a+b=( )
| A. | 0 | B. | 1 | C. | -1 | D. | 2 |