题目内容
15.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的右焦点为F(2,0),设A,B为双曲线上关于原点对称的两点,且满足$\overrightarrow{AF}•\overrightarrow{BF}=0$,若直线AB的斜率为$\sqrt{3}$,则双曲线的离心率为$\sqrt{3}+1$.分析 设A(x1,y1),则B(-x1,-y1),满足$\overrightarrow{AF}•\overrightarrow{BF}=0$,再由点A在双曲线上且直线AB的斜率,得到关于x1、y1、a、b的方程组,联解消去x1、y1得到关于a、b的等式,结合b2+a2=c2解出a=$\sqrt{3}$-1,可得离心率e的值.
解答 解:根据题意,设A(x1,y1),则B(-x1,-y1),
∵焦点F(2,0),$\overrightarrow{AF}•\overrightarrow{BF}=0$,
可得$\overrightarrow{AF}$•$\overrightarrow{BF}$=(x1-2)(-x1-2)-y12=0,
即为x12+y12=4,…①
又∵点A在双曲线上,且直线AB的斜率为$\sqrt{3}$,
∴$\left\{\begin{array}{l}{\frac{{x}_{1}^{2}}{{a}^{2}}-\frac{{y}_{1}^{2}}{{b}^{2}}=1}\\{{y}_{1}=\sqrt{3}{x}_{1}}\end{array}\right.$,…②.
由①②联解消去x1、y1,得$\frac{1}{{a}^{2}}$-$\frac{3}{{b}^{2}}$=1,…③
又∵F(2,0)是双曲线的右焦点,可得b2=c2-a2=4-a2,
∴代入③,化简整理得a4-8a2+4=0,解之得a2=4+2$\sqrt{3}$或4-2$\sqrt{3}$,
由于a2<c2=4,所以a2=4+2$\sqrt{3}$不合题意,舍去.
∴a2=4-2$\sqrt{3}$=($\sqrt{3}$-1)2,
∴a=$\sqrt{3}$-1,
∴离心率e=$\frac{c}{a}$=$\frac{2}{\sqrt{3}-1}$=$\sqrt{3}$+1,
故答案为:$\sqrt{3}$+1
点评 本题给出双曲线满足的条件,求它的离心率,着重考查了双曲线的标准方程与简单几何性质等知识,属于中档题.熟练掌握双曲线的标准方程及其性质、参数a、b、c的关系,是解决本题的关键.

| A. | {2} | B. | {0,2} | C. | {0,1,2,3,4,6} | D. | {1,2,3,4,6} |
| A. | 若l∥α,l⊥m,则m⊥α | B. | 若l∥α,l⊥m,m?β,则α⊥β | ||
| C. | 若l∥α,l∥m,则m∥α | D. | 若α∥β,l∥α,l∥m,m?β,则m∥β |
| A. | $\sqrt{2}$ | B. | -$\sqrt{2}$ | C. | 1 | D. | 0 |
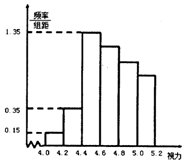 某校高一共录取新生1000名,为了解学生视力情况,校医随机抽取了100名学生进行视力测试,并得到如下频率分布直方图.
某校高一共录取新生1000名,为了解学生视力情况,校医随机抽取了100名学生进行视力测试,并得到如下频率分布直方图.(Ⅰ)若视力在4.6~4.8的学生有24人,试估计高一新生视力在4.8以上的人数;
| 1~50名 | 951~1000名 | |
| 近视 | 41 | 32 |
| 不近视 | 9 | 18 |
(Ⅲ)用分层抽样的方法从(Ⅱ)中27名不近视的学生中抽出6人,再从这6人中任抽2人,其中抽到成绩在前50名的学生人数为ξ,求ξ的分布列和数学期望.
附:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
| P(K2≥k) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |