题目内容

求下列三角函数值：
（1）cos（-1050°）；
（2）tan
19π
3
；
（3）sin（-
31π
4
）．
考点：运用诱导公式化简求值
专题：三角函数的求值
分析：由条件利用诱导公式化简所给的各个式子，求得结果．
解答： 解：（1）cos（-1050°）=cos[（-3×360°）+30°]=cos30°=
3
2
．
（2）tan
19π
3
=tan（6π+
π
3
）=tan
π
3
=
3
．
（3）sin（-
31π
4
）=sin[（-8π）+
π
4
]=sin
π
4
=
2
2
．
点评：本题主要考查利用诱导公式进行化简求值，属于基础题．
练习册系列答案
相关题目
已知函数f（x）的定义域为R，对任意实数u，v满足f（u+v）=f（u）+f（v），且f（uv）=uf（v）+vf（u）．用含u、v、f（u）、f（v）的表达式来表示f（
u
v
）=
 
．
下列说法不正确的是（　　）
A、命题“对?x∈R，都有x2≥0”的否定为“?x0∈R，使得x02＜0”
B、“a＞b”是“ac2＞bc2”的必要不充分条件
C、“若tanα≠
3
，则α≠
π
3
”是真命题
D、甲、乙两位学生参与数学模拟考试，设命题p是“甲考试及格”，q是“乙考试及格”，则命题“至少有一位学生不及格”可表示为（￢p）∧（￢q）
已知函数g（x）=b2lnx-bx-3（b∈R）的极值点为x=1，函数h（x）=ax2+bx+4b-1．
（Ⅰ）求函数g（x）的单调区间，并比较g（x）与g（1）的大小关系；
（Ⅱ）当a=
1
2
时，函数t（x）=ln（1+x2）-h（x）+x+4-k（k∈R），试判断函数t（x）的零点个数；
（Ⅲ）如果函数f（x），f1（x），f2（x）在公共定义域D上，满足f1（x）＜f（x）＜f2（x），那么就称f（x）为f1（x），f2（x）的“伴随函数”，已知函数f1（x）=（a-
1
2
）x2+2ax+（1-a2）lnx，f2（x）=
1
2
x2+2ax，若在区间（1，+∞）上，函数f（x）=g（x）+h（x）是f1（x），f2（x）的“伴随函数”，求a的取值范围．
求圆（x-1）2+（y+2）2=4上的一点Q到点P（-
4
5
，
2
5
）的最短距离及这个点的坐标．
设非空集合A，若对A中任意两个元素a，b，通过某个法则“•”，使A中有唯一确定的元素c与之对应，则称法则“•”为集合A上的一个代数运算．若A上的代数运算“•”还满足：（1）对?a，b，c∈A，都有（a•b）•c=a•（b•c）；（2）对?a∈A，?e，b∈A，使得e•a=a•e=a，a•b=b•a=e．称A关于法则“•”构成一个群．给出下列命题：
①实数的除法是实数集上的一个代数运算；
②自然数集关于自然数的加法不能构成一个群；
③非零有理数集关于有理数的乘法构成一个群；
④正整数集关于法则a°b=ab构成一个群．
其中正确命题的序号是
 
．（填上所有正确命题的序号）．
已知幂函数f（x）=xα的图象过点(2，
2
2
)，则f（16）=
 
．
某市统计局就某地居民的月收入调查了10000人，并根据所得数据画出样本的频率分布直方图如图所示．（每个分组包括左端点，不包括右端点，如第一组表示[1000，1500））

（Ⅰ）求居民收入在[1500，2500）的频率；
（Ⅱ）为了分析居民的收入与年龄、职业等方面的关系，必须按月收入再从这10000人中按分层抽样方法抽出100人作进一步分析，则月收入在[2500，3000）的这段应抽取多少人？
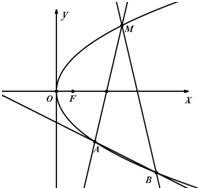已知点F为抛物线C：y2=2px（p＞0）的焦点，M（4，t）（t＞0）为抛物线C上的点，且|MF|=5．
（Ⅰ）求抛物线C的方程和点M的坐标；
（Ⅱ）过点M引出斜率分别为k1，k2的两直线l1，l2，l1与抛物线C的另一交点为A，l2与抛物线C的另一交点为B，记直线AB的斜率为k3．
（ⅰ）若k1+k2=0，试求k3的值；
（ⅱ）证明：
1
k1
+
1
k2
-
1
k3
为定值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网