题目内容
20.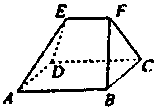 如图,在多面体ABCDEF中,四边形ABCD是边长为3的正方形,EF∥AB,EF=$\frac{3}{2}$,且点E到平面ABCD的距离为2,则该多面体的体积为( )
如图,在多面体ABCDEF中,四边形ABCD是边长为3的正方形,EF∥AB,EF=$\frac{3}{2}$,且点E到平面ABCD的距离为2,则该多面体的体积为( )| A. | $\frac{9}{2}$ | B. | 5 | C. | 6 | D. | $\frac{15}{2}$ |
分析 法一:取AB中点G,CD中点H,连结GE、GH、EH,该多面体的体积VABCDEF=VBCF-GHE+VE-AGHD,由此能求出结果.
法二:连接BE、CE,求出四棱锥E-ABCD的体积VE-ABCD=6,由整个几何体大于四棱锥E-ABCD的体积,能求出结果.
解答  解法一:取AB中点G,CD中点H,连结GE、GH、EH,
解法一:取AB中点G,CD中点H,连结GE、GH、EH,
∵在多面体ABCDEF中,四边形ABCD是边长为3的正方形,
EF∥AB,EF=$\frac{3}{2}$,且点E到平面ABCD的距离为2,
∴该多面体的体积:
VABCDEF=VBCF-GHE+VE-AGHD
=S△BCF×EF+$\frac{1}{3}{S}_{矩形AGHD}×2$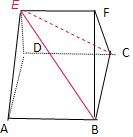
=$\frac{1}{2}×3×2×\frac{3}{2}$+$\frac{1}{3}×3×\frac{3}{2}×2$=$\frac{15}{2}$.
故选:D.
解法二:如下图所示,连接BE、CE
则四棱锥E-ABCD的体积VE-ABCD=$\frac{1}{3}$×3×3×2=6,
又∵整个几何体大于四棱锥E-ABCD的体积,
∴所求几何体的体积VABCDEF>VE-ABCD,
故选:D.
点评 本题考查多面体的体积的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
10.某班对一次实验成绩进行分析,利用随机数表法抽取样本时,先将50个同学按01,02,03…50进行编号,然后从随机数表第9行第11列的数开始向右读,则选出的第7个个体是( )
(注:表为随机数表的第8行和第9行)

(注:表为随机数表的第8行和第9行)

| A. | 02 | B. | 13 | C. | 42 | D. | 44 |
15.直线mx+$\frac{n}{2}$y-1=0在y轴上的截距是-1,且它的倾斜角是直线$\sqrt{3}x-y-3\sqrt{3}$=0的倾斜角的2倍,则( )
| A. | m=-$\sqrt{3}$,n=-2 | B. | m=$\sqrt{3}$,n=2 | C. | m=$\sqrt{3}$,n=-2 | D. | m=-$\sqrt{3}$,n=2 |
12.“x>0”是“(x-2)(x-4)<0”成立的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
9.如图所示是用模拟方法估计圆周率π值的程序框图,m表示估计结果,则图中空白处应填入( )
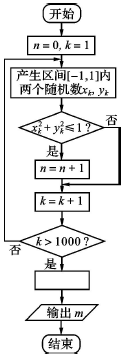

| A. | $m=1-\frac{n}{1000}$ | B. | $m=\frac{n}{1000}$ | C. | $m=1-\frac{n}{250}$ | D. | $m=\frac{n}{250}$ |
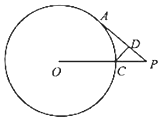 如图,过圆O外一点P作圆O的切线PA,切点为A,连接OP与圆O交于点C,过点C作圆O作AP的垂线,垂足为D,若PA=2$\sqrt{5}$,PC:PO=1:3,求CD的长.
如图,过圆O外一点P作圆O的切线PA,切点为A,连接OP与圆O交于点C,过点C作圆O作AP的垂线,垂足为D,若PA=2$\sqrt{5}$,PC:PO=1:3,求CD的长.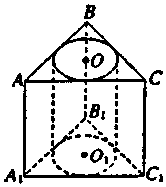 如图,三棱柱ABC-A1B1C1的侧棱垂直于底面,其高为6cm,底面三角形的边长分别为3cm,4cm,5cm,以上、下底面的内切圆为底面,挖去一个圆柱,求剩余部分几何体的体积V.
如图,三棱柱ABC-A1B1C1的侧棱垂直于底面,其高为6cm,底面三角形的边长分别为3cm,4cm,5cm,以上、下底面的内切圆为底面,挖去一个圆柱,求剩余部分几何体的体积V.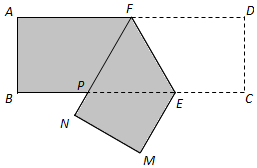 如图,某机械厂要将长6m,宽2m的长方形铁皮ABCD进行裁剪.已知点F为AD的中点,点E在边BC上,裁剪时先将四边形CDFE沿直线EF翻折到MNFE处(点C,D分别落在直线BC下方点M,N处,FN交边BC于点P),再沿直线PE裁剪.
如图,某机械厂要将长6m,宽2m的长方形铁皮ABCD进行裁剪.已知点F为AD的中点,点E在边BC上,裁剪时先将四边形CDFE沿直线EF翻折到MNFE处(点C,D分别落在直线BC下方点M,N处,FN交边BC于点P),再沿直线PE裁剪.