题目内容
8．
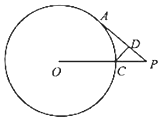如图，过圆O外一点P作圆O的切线PA，切点为A，连接OP与圆O交于点C，过点C作圆O作AP的垂线，垂足为D，若PA=2$\sqrt{5}$，PC：PO=1：3，求CD的长．
分析 连接OA，延长PO与圆相交于点B，由PA与⊙O相切于点A，可得OA⊥AP，又CD⊥AP，则CD∥OA．可得$\frac{CD}{OA}$=$\frac{PC}{PO}$=$\frac{1}{3}$．设PC=x，则OC=2x=OB，由切割线定理可得：PA2=PC•PB，解得x，即可得出．
解答 解：连接OA，延长PO与圆相交于点B，
∵PA与⊙O相切于点A，∴OA⊥AP，
又CD⊥AP，则CD∥OA．
∴$\frac{CD}{OA}$=$\frac{PC}{PO}$=$\frac{1}{3}$．
设PC=x，则OC=2x=OB，
由切割线定理可得：PA2=PC•PB，
∴x•5x=$（2\sqrt{5}）^{2}$，解得x=2．
∴CD=$\frac{1}{3}OA$=$\frac{1}{3}×4$=$\frac{4}{3}$．
点评 本题考查了切割线定理、圆的切线的性质、平行线的性质定理，考查了推理能力与计算能力，属于中档题．
练习册系列答案
优学名师名题系列答案
相关题目
在ABC-A1B1C1中，所有棱长均相等，且∠ABB1=60°，D为AC的中点，求证：
13．设l，m，n表示三条直线，α，β，γ表示三个平面，则下面命题中不成立的是（ ）
| A． | 若l⊥α．m⊥α，则l∥m | |
| B． | 若m?β，m⊥l，n是l在β内的射影，则m⊥n | |
| C． | 若m?α，n?α，m∥n，则n∥α | |
| D． | 若α⊥γ，β⊥γ，则α∥β． |
20．
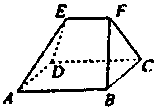如图，在多面体ABCDEF中，四边形ABCD是边长为3的正方形，EF∥AB，EF=$\frac{3}{2}$，且点E到平面ABCD的距离为2，则该多面体的体积为（ ）
如图，在多面体ABCDEF中，四边形ABCD是边长为3的正方形，EF∥AB，EF=$\frac{3}{2}$，且点E到平面ABCD的距离为2，则该多面体的体积为（ ）| A． | $\frac{9}{2}$ | B． | 5 | C． | 6 | D． | $\frac{15}{2}$ |