题目内容
9．如图所示是用模拟方法估计圆周率π值的程序框图，m表示估计结果，则图中空白处应填入（ ）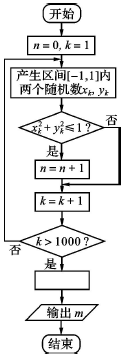
| A． | $m=1-\frac{n}{1000}$ | B． | $m=\frac{n}{1000}$ | C． | $m=1-\frac{n}{250}$ | D． | $m=\frac{n}{250}$ |
分析 由题意以及框图的作用，直接推断空白框内应填入的表达式．
解答 解：由题意以及程序框图可知，
用模拟方法估计圆周率π的程序框图，n是圆周内的点的次数，当i大于1000时，
圆周内的点的次数为4n，总试验次数为1000，
所以要求的概率 $\frac{4n}{1000}$，
所以空白框内应填入的表达式是m=$\frac{4n}{1000}$=$\frac{n}{250}$．
故选：D．
点评 本题考查程序框图的作用，考查模拟方法估计圆周率π的方法，考查计算能力，属于基础题．
练习册系列答案
备战中考寒假系列答案
相关题目
20．
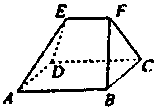如图，在多面体ABCDEF中，四边形ABCD是边长为3的正方形，EF∥AB，EF=$\frac{3}{2}$，且点E到平面ABCD的距离为2，则该多面体的体积为（ ）
如图，在多面体ABCDEF中，四边形ABCD是边长为3的正方形，EF∥AB，EF=$\frac{3}{2}$，且点E到平面ABCD的距离为2，则该多面体的体积为（ ）| A． | $\frac{9}{2}$ | B． | 5 | C． | 6 | D． | $\frac{15}{2}$ |
4．命题?x＞0，ln（x+1）＞0的否定为（ ）
| A． | ?x0＜0，ln（x0+1）＜0 | B． | ?x0≤0，ln（x0+1）≤0 | C． | ?x0＞0，ln（x0+1）＜0 | D． | ?x0＞0，ln（x0+1）≤0 |
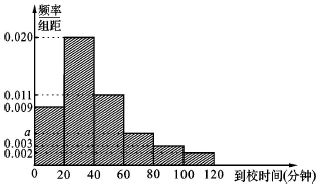某校收集该校学生从家到学校的时间后，制作成如下的频率分布直方图：