题目内容
方程:9x+4x=
•6x的解集为 .
| 5 |
| 2 |
考点:函数的零点
专题:函数的性质及应用
分析:将方程转化为∴(2•3x-2x)(3x-2•2x)=0,解出即可.
解答:
解:由9x+4x=
•6x,得:32x+22x=
•3x•2x,
∴(2•3x-2x)(3x-2•2x)=0,
∴3x=2x-1或3x=2x+1,
解得:x=
或x=-
,
故答案为:{x|x=
或x=-
}.
| 5 |
| 2 |
| 5 |
| 2 |
∴(2•3x-2x)(3x-2•2x)=0,
∴3x=2x-1或3x=2x+1,
解得:x=
| ||
|
| ||
|
故答案为:{x|x=
| ||
|
| ||
|
点评:本题考查了用因式分解求解方程问题,考查了指数,对数的互化问题,是一道中档题.

练习册系列答案
相关题目
已知{an}为等差数列,若
<-1,且它的前n项和Sn有最小值,那么当Sn取到最小正值时,n=( )
| a15 |
| a14 |
| A、14 | B、27 | C、28 | D、29 |
如果一个棱锥的各个侧面都是等边三角形,那么这个棱锥不可能是( )
| A、三棱锥 | B、四棱锥 |
| C、五棱锥 | D、六棱锥 |
以下表示正确的是( )
| A、∅=0 | B、∅={0} |
| C、∅∈{0} | D、∅⊆{0} |
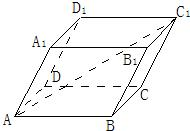 如图,在平行六面体ABCD-A1B1C1D1中,AB=1,AD=2,AA1=3,AC1=5,∠BAD=∠BAA1=60°,求∠DAA1的大小.
如图,在平行六面体ABCD-A1B1C1D1中,AB=1,AD=2,AA1=3,AC1=5,∠BAD=∠BAA1=60°,求∠DAA1的大小.