题目内容
已知α是锐角.
(1)求证:1<sinα+cosα<
;
(2)利用单位圆中的三角函数线求同时满足sinα≤
,cos≥
的α的取值范围.
(1)求证:1<sinα+cosα<
| π |
| 2 |
(2)利用单位圆中的三角函数线求同时满足sinα≤
| ||
| 2 |
| ||
| 2 |
考点:三角函数线
专题:三角函数的图像与性质
分析:(1)利用单位圆与三角函数线,结合图形即可证明;
(2)画出图形,结合单位圆中的三角函数线,写出α的取值范围.
(2)画出图形,结合单位圆中的三角函数线,写出α的取值范围.
解答:
 解:(1)证明:∵α为锐角,α的终边落在第一象限内,
解:(1)证明:∵α为锐角,α的终边落在第一象限内,
设α的终边与单位圆交于点P(x,y)时,过P作PM⊥x轴于点M,作PN⊥Y轴于点N(如图),
则sinα=MP,cosα=OM=NP,
利用三角形两边之和大于第三边得:sinα+cosα=MP+OM>1;
又∵sinα+cosα=MP+OM<
+
=
=
,
∴1<sinα+cosα<
.
(2)画出图形,如图所示;
单位圆中的三角函数线同时满足sinα≤
,cos≥
的α是
;
即α的取值范围是{-
+2kπ≤x≤
+2kπ,k∈Z}.
 解:(1)证明:∵α为锐角,α的终边落在第一象限内,
解:(1)证明:∵α为锐角,α的终边落在第一象限内,设α的终边与单位圆交于点P(x,y)时,过P作PM⊥x轴于点M,作PN⊥Y轴于点N(如图),
则sinα=MP,cosα=OM=NP,
利用三角形两边之和大于第三边得:sinα+cosα=MP+OM>1;
又∵sinα+cosα=MP+OM<
 |
| PA |
 |
| PB |
 |
| AB |
| π |
| 2 |
∴1<sinα+cosα<
| π |
| 2 |
(2)画出图形,如图所示;
单位圆中的三角函数线同时满足sinα≤
| ||
| 2 |
| ||
| 2 |

|
即α的取值范围是{-
| π |
| 6 |
| π |
| 6 |
点评:本题考查任意角的三角函数的定义,用单位圆中的三角函数线表示三角函数的值的应用问题,考查了数形结合方法的应用问题,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知等差数列{an}中,a2+a4=6,则前5项和S5为( )
| A、5 | B、6 | C、15 | D、30 |
直线x+y+1=0的倾斜角为( )
| A、135° | B、120° |
| C、60° | D、45° |
已知函数y=
,则( )
| x-2 |
| x-1 |
| A、(-∞,1)是函数的递增区间 |
| B、(-∞,-1)是函数的递减区间 |
| C、(-1,+∞)是函数的递增区间 |
| D、(1,+∞)是函数的递减区间 |
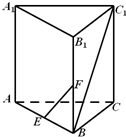 如图,在直三棱柱ABC-A1B1C1中,AA1=AB=BC,∠ABC=90°,点E,F分别是棱AB,BB1的中点,则直线EF和BC1所成的角是( )
如图,在直三棱柱ABC-A1B1C1中,AA1=AB=BC,∠ABC=90°,点E,F分别是棱AB,BB1的中点,则直线EF和BC1所成的角是( )| A、45° | B、135° |
| C、60° | D、120° |