题目内容
已知椭圆的一个焦点坐标为(3,0),椭圆的长轴长为10,求椭圆的标准方程.
考点:椭圆的标准方程
专题:圆锥曲线的定义、性质与方程
分析:由椭圆的一个焦点为(3,0),长轴长为10,中心在坐标原点,知2a=10,c=3,由此能求出b,即可求出椭圆的标准方程.
解答:
解:∵椭圆的一个焦点为(3,0),长轴长为10,中心在坐标原点,
∴2a=10,即a=5,c=3,b=
=4
∴此椭圆的标准方程:
+
=1.
∴2a=10,即a=5,c=3,b=
| 52-32 |
∴此椭圆的标准方程:
| x2 |
| 25 |
| y2 |
| 16 |
点评:本题考查椭圆的简单性质的应用,是基础题.解题时要认真审题,仔细解答.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
在等差数列{an}中,a1+a9=10,a4=4,则a6=( )
| A、2 | B、4 | C、6 | D、8 |
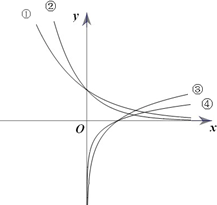 如图,设实数a,b,c,d>0,且不等于1,曲线①,②,③,④分别表示函数y=ax,y=bx,y=logcx,y=logdx在同一坐标系中的图象,则a,b,c,d的大小顺序为
如图,设实数a,b,c,d>0,且不等于1,曲线①,②,③,④分别表示函数y=ax,y=bx,y=logcx,y=logdx在同一坐标系中的图象,则a,b,c,d的大小顺序为