Question

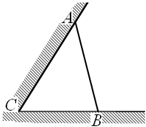如图所示，某建筑工地准备建造一间两面靠墙的三角形露天仓库堆放材料，已知已有两面墙CA、CB的夹角为60°（即∠ACB=60°），现有可供建造第三面围墙的材料6米（两面墙的长均大于6米），为了使得仓库的面积尽可能大，记∠ABC=θ，问当θ为多少时，所建造的三角形露天仓库的面积最大，并求出最大值？

Answer 1

考点：正弦定理,解三角形的实际应用

专题：三角函数的求值

分析：在三角形ABC中，利用正弦定理列出关系式，表示出AC与BC，利用三角形面积公式表示出三角形ABC面积，整理后根据正弦函数的值域即可确定出三角形ABC面积的最大值，以及此时θ的值．

解答： 解：在△ABC中，由正弦定理：

AC

sinθ

=

AB

sin π 3

=

BC

sin( 2π 3 -θ)

，
化简得：AC=

ABsinθ

sin π 3

=

6sinθ

3 2

=4

3

sinθ，BC=

ABsin( 2π 3 -θ)

sin π 3

=

6sin( 2π 3 -θ)

3 2

=4

3

sin（

2π

3

-θ）=4

3

sin（θ+

π

3

），
∴S_△ABC=

1

2

AC•BC•sin

π

3

=12

3

sinθsin（θ+

π

3

）
=12

3

sinθ（

1

2

sinθ+

3

2

cosθ）
=6

3

（sin²θ+

3

sinθcosθ）
=6

3

（

1-cos2θ

2

+

3

2

sin2θ）      
=6

3

sin（2θ-

π

6

）+3

3

，
∵0＜θ＜

2π

3

，
∴当2θ-

π

6

=

π

2

，即θ=

π

3

时，（S_△ABC）_max=9

3

，
答：当θ=60°时，所建造的三角形露天仓库的面积最大且值为9

3

m²．

点评：此题考查了正弦定理，以及解三角形的实际应用，熟练掌握正弦定理是解本题的关键．