题目内容
已知实数x,y满足
时,z=
+
(a≥b>0)的最大值为1,则a+b的最小值为( )
|
| x |
| a |
| y |
| b |
| A、7 | B、8 | C、9 | D、10 |
考点:简单线性规划
专题:不等式的解法及应用
分析:作出不等式组对应的平面区域,利用z的最大值,确定最优解,然后利用基本不等式进行判断.
解答:
解:作出不等式组对应的平面区域如图:
由z=
+
(a≥b>0)得y=-
x+bz,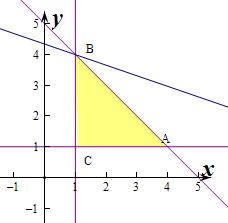
则斜率k=-
∈[-1,0),
则由图象可知当直线y=-
x+bz经过点B(1,4)时,
直线y=-
x+bz的截距最大,
此时
+
=1,
则a+b=(a+b)(
+
)=1+4+
+
≥5+2
=5+4=9,
当且仅当
=
,即b=2a取等号此时不成立,故基本不等式不成立.
设t=
,
∵a≥b>0,
∴0<
≤1,即0<t≤1,
则1+4+
+
=5+t+
在(0,1]上单调递减,
∴当t=1时,
1+4+
+
=5+t+
取得最小值为
5+1+4=10.
即a+b的最小值为10,
故选:D.
由z=
| x |
| a |
| y |
| b |
| b |
| a |

则斜率k=-
| b |
| a |
则由图象可知当直线y=-
| b |
| a |
直线y=-
| b |
| a |
此时
| 1 |
| a |
| 4 |
| b |
则a+b=(a+b)(
| 1 |
| a |
| 4 |
| b |
| b |
| a |
| 4a |
| b |
|
当且仅当
| b |
| a |
| 4a |
| b |
设t=
| b |
| a |
∵a≥b>0,
∴0<
| b |
| a |
则1+4+
| b |
| a |
| 4a |
| b |
| 4 |
| t |
∴当t=1时,
1+4+
| b |
| a |
| 4a |
| b |
| 4 |
| t |
5+1+4=10.
即a+b的最小值为10,
故选:D.
点评:本题主要考查线性规划和基本不等式的应用,先利用条件确定最优解是解决本题的关键,本题使用基本不等式时,条件不成立,利用t+
的单调性是解决本题的关键,综合性较强,难度较大.
| 4 |
| t |

练习册系列答案
相关题目
下列说法正确的是( )
| A、若p且q为假命题,则p,q均为假命题 |
| B、“x>2”是“x2-3x+2>0”的必要不充分条件 |
| C、若m<1,则方程x2-2x+m=0无实数根 |
| D、命题“若x=y,则sinx=siny”的逆否命题为真命题 |
已知m,n为异面直线,m⊥平面α,n⊥平面β.直线l满足l⊥m,l⊥n,l?α,l?β,则( )
| A、α与β相交,且交线平行于l |
| B、α与β相交,且交线垂直于l |
| C、α∥β,且l∥α |
| D、α⊥β,且l⊥β |
已知l,m,n是三条不同的直线,α,β是不同的平面,则下列条件中能推出α⊥β的是( )
| A、l?α,m?β,且l⊥m |
| B、l?α,m?β,n?β,且l⊥m,l⊥n |
| C、m?α,n?β,m∥n,且l⊥m |
| D、l?α,l∥m,且m⊥β |
若复数z满足:iz=3+4i,则z=( )
| A、-3-4i | B、4+3i |
| C、4-3i | D、-4+3i |