题目内容
已知m,n为异面直线,m⊥平面α,n⊥平面β.直线l满足l⊥m,l⊥n,l?α,l?β,则( )
| A、α与β相交,且交线平行于l |
| B、α与β相交,且交线垂直于l |
| C、α∥β,且l∥α |
| D、α⊥β,且l⊥β |
考点:空间中直线与平面之间的位置关系
专题:综合题,空间位置关系与距离
分析:由题目给出的已知条件,结合线面平行,线面垂直的判定与性质,可以直接得到正确的结论.
解答:
解:由m⊥平面α,直线l满足l⊥m,且l?α,所以l∥α,
又n⊥平面β,l⊥n,l?β,所以l∥β.
由直线m,n为异面直线,且m⊥平面α,n⊥平面β,则α与β相交,否则,若α∥β则推出m∥n,
与m,n异面矛盾.
故α与β相交,且交线平行于l.
故选:A.
又n⊥平面β,l⊥n,l?β,所以l∥β.
由直线m,n为异面直线,且m⊥平面α,n⊥平面β,则α与β相交,否则,若α∥β则推出m∥n,
与m,n异面矛盾.
故α与β相交,且交线平行于l.
故选:A.
点评:本题考查了平面与平面之间的位置关系,考查了平面的基本性质及推论,考查了线面平行、线面垂直的判定与性质,考查了学生的空间想象和思维能力,是中档题.

练习册系列答案
相关题目
设平面α、β,直线a、b,a?α,b?α,则“a∥β,b∥β”是“α∥β”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
下列四个结论:
(1)两条直线都和同一个平面平行,则这两条直线平行;
(2)两条直线没有公共点,则这两条直线平行;
(3)两条直线都和第三条直线垂直,则这两条直线平行;
其中正确的命题个数为( )
(1)两条直线都和同一个平面平行,则这两条直线平行;
(2)两条直线没有公共点,则这两条直线平行;
(3)两条直线都和第三条直线垂直,则这两条直线平行;
其中正确的命题个数为( )
| A、0 | ||
| B、1 | ||
| C、π | ||
D、
|
已知实数x,y满足
时,z=
+
(a≥b>0)的最大值为1,则a+b的最小值为( )
|
| x |
| a |
| y |
| b |
| A、7 | B、8 | C、9 | D、10 |
执行如图所示的程序框图,则输出S的值为( )
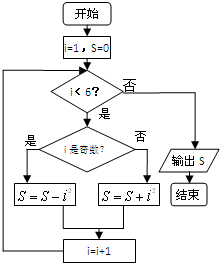

| A、3 | B、-6 | C、10 | D、-15 |