题目内容
5.已知△ABC是锐角三角形,内角A、B、C所对的边分别是a、b、c,满足${sin}^{2}A=sin(\frac{π}{3}+B)sin(\frac{π}{3}-B)+{sin}^{2}$B.(Ⅰ)求角A的值;
(Ⅱ)若$\overrightarrow{AB}•\overrightarrow{AC}$=12,a=2$\sqrt{7}$,求△ABC的周长.
分析 (Ⅰ)利用条件以及三角恒等变换求得sinA的值,可得A的值.
(Ⅱ)由条件求得bc的值,再利用余弦定理求得b+c的值,可得,△ABC的周长.
解答 解:(Ⅰ)△ABC是锐角三角形,${sin}^{2}A=(sin\frac{π}{3}cosB+cos\frac{π}{3}sinB)(sin\frac{π}{3}cosB-cos\frac{π}{3}sinB)+{sin}^{2}B$
=$\frac{3}{4}{cos^2}B-\frac{1}{4}{sin^2}B+{sin^2}B=\frac{3}{4}$,
∴$sinA=±\frac{{\sqrt{3}}}{2}$.
又A为锐角,所以$A=\frac{π}{3}$.
(Ⅱ)由$\overrightarrow{AB}•\overrightarrow{AC}=12$,得bccosA=12 ①,
由(1)知$A=\frac{π}{3}$,所以bc=24 ②,
由余弦定理知a2=b2+c2-2bccosA,将$a=2\sqrt{7}$及①代入可得c2+b2=52 ③,
③+②×2,得(c+b)2=100,所以c+b=10,△ABC的周长是$10+2\sqrt{7}$.
点评 本题主要考查三角恒等变换,两个向量的数量积的运算,余弦定理的应用,属于中档题.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
17.函数$y=Asin({ωx+φ})({A>0,ω>0,|φ|<\frac{π}{2}})$的部分图象如图所示,则( )
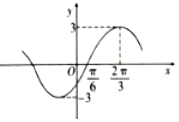

| A. | $y=3sin({2x-\frac{π}{6}})$ | B. | $y=3sin({2x-\frac{π}{3}})$ | C. | $y=3sin({x-\frac{π}{6}})$ | D. | $y=3sin({x-\frac{π}{3}})$ |
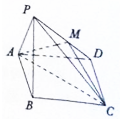 如图,已知四棱锥P-ABCD,底面ABCD为菱形,且∠DAB=60°,△PAB是边长为a的正三角形,且平面PAB⊥平面ABCD,已知点M是PD的中点.
如图,已知四棱锥P-ABCD,底面ABCD为菱形,且∠DAB=60°,△PAB是边长为a的正三角形,且平面PAB⊥平面ABCD,已知点M是PD的中点.